Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) An: "\(\forall x \in \mathbb R ,{x^2} \ge 0\)"
b) Bình: "\(\exists x \in ,{x^2} < 0\)"

hình :
ta có : \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AD}+\overrightarrow{CD}\right)^2=\left(\overrightarrow{AC}+\overrightarrow{BD}\right)^2\)
\(\Leftrightarrow AB^2+BC^2+AD^2+CD^2+2\overrightarrow{AB}.\overrightarrow{BC}+2\overrightarrow{BC}.\overrightarrow{AD}+2\overrightarrow{AD}.\overrightarrow{CD}+2\overrightarrow{CD}.\overrightarrow{AB}=AC^2+BD^2+2\overrightarrow{AC}.\overrightarrow{BD}\)
\(\Leftrightarrow AB^2+BC^2+AD^2+CD^2+2\overrightarrow{BC}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)+2\overrightarrow{CD}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=AC^2+BD^2+2\overrightarrow{AC}.\overrightarrow{BD}\)
\(\Leftrightarrow AB^2+BC^2+AD^2+CD^2+2\overrightarrow{BC}.\overrightarrow{AC}+2\overrightarrow{CD}.\overrightarrow{AC}=AC^2+BD^2+2\overrightarrow{AC}.\overrightarrow{BD}\)\(\Leftrightarrow AB^2+BC^2+AD^2+CD^2+2\overrightarrow{AC}\left(\overrightarrow{BC}+\overrightarrow{CD}\right)=AC^2+BD^2+2\overrightarrow{AC}.\overrightarrow{BD}\) \(\Leftrightarrow AB^2+BC^2+AD^2+CD^2+2\overrightarrow{AC}.\overrightarrow{BD}=AC^2+BD^2+2\overrightarrow{AC}.\overrightarrow{BD}\) \(\Rightarrow AB^2+BC^2+AD^2+CD^2=AC^2+BD^2\)
vậy tổng bình phương các cạch bằng tổng bình phương của 2 đường chéo (đpcm)

giả sử ta có hình bình hành ABCD
ta có \(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\Rightarrow AC^2=AB^2+BC^2+2.AB.BC.cos\left(BAD\right)\)
\(\overrightarrow{BD}=\overrightarrow{BC}+\overrightarrow{CD}\Rightarrow BD^2=BC^2+CD^2+2BC.CDcos\left(ABC\right)\)
Nên \(AC^2+BD^2=AB^2+BC^2+CD^2+AD^2+2AB.BC.\left[cos\left(ABC\right)+cos\left(BAD\right)\right]\)
\(=AB^2+BC^2+CD^2+AD^2\)
do đó ta có điều phải chứng minh

Trong tiết học môn Toán, Nam phát biểu: “Mọi số thực đều có bình phương khác 1”.
Mai phát biểu: “Có một số thực mà bình phương của nó bằng 1”
a) Phát biểu của Nam là sai. (chẳng hạn 1 và -1)
Phát biểu của Mai là đúng, số thực đó là 1 và -1.
b) Phát biểu của Nam: "\(\forall x \in \mathbb{R},\;{x^2} \ne 1\)".
Phát biểu của Mai: "\(\exists \;x \in \mathbb{R},{x^2} = 1\)".

Thay \(\left(-2;2\right)\) vào 2 pt 2 cạnh đều ko thỏa \(\Rightarrow\) 2 cạnh còn lại đi qua (-2;2)
2 cạnh đã cho ban đầu có vtpt lần lượt là (1;-1) và (1;3), do đó 2 cạnh còn lại cũng lần lượt nhận (1;-1) cà (1;3) là vtpt (do các cặp cạnh đối của hình bình hành song song)
Phương trình 2 cạnh còn lại là:
\(1\left(x+2\right)-1\left(y-2\right)=0\Leftrightarrow x-y+4=0\)
\(1\left(x+2\right)+3\left(y-2\right)=0\Leftrightarrow x+3y-4=0\)

a) “\(\forall x \in \mathbb{R},x + ( - x) = 0\)”
b) “\(\exists n \in \mathbb{N},{x^2} = 9\)”
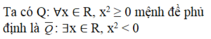
1.Bình phương của 1 tổng bằng bình phương số thứ 1 cộng hai lần tích của số thứ nhất với số thứ hai cộng bình phương số thứ hai
2.Bình phương của 1 hiệu bằng bình phương số thứ 1 trừ 2 lần tích số thứ nhất với số thứ 2 cộng với bình phương số thứ 2.
3.Hiệu 2 bình phương bằng tích của tổng 2 số với hiệu 2 số.
4.Lập phương của 1 tổng bằng lập phương số thứ 1 + 3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 + lập phương số thứ 2.
5. Lập phương của 1 tổng bằng lập phương số thứ 1 -3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 - lập phương số thứ 2.
6.Tổng hai lập phương bằng tích giữa tổng 2 số với bình phương thiếu của 1 hiệu.
7.Hiệu 2 lập phương bằng tích giữa hiệu hai số với bình phương thiếu của 1 tổng.
ko hiểu đề bài cho lắm >:(