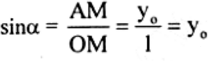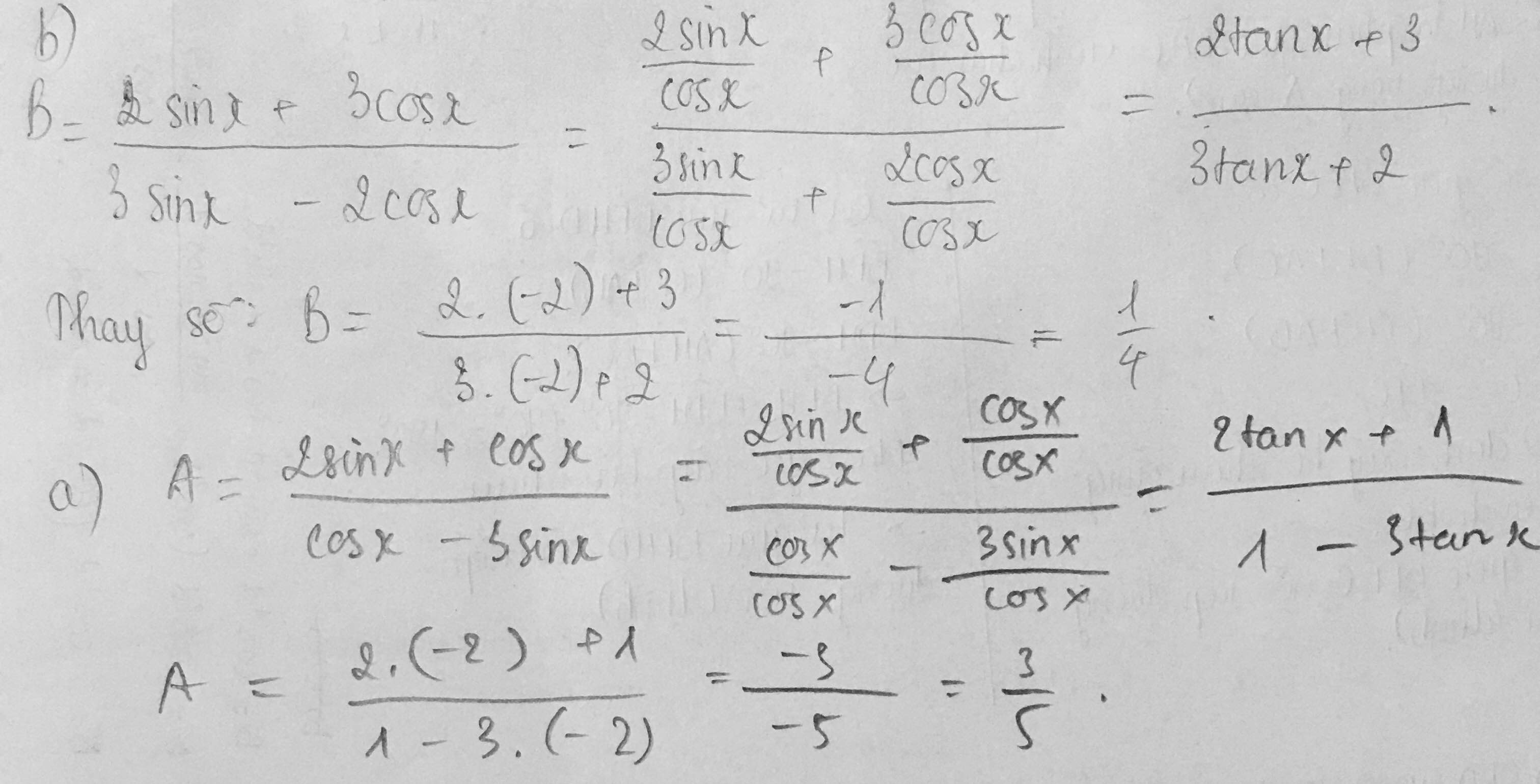Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

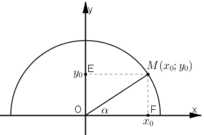
a) Trên nửa đường tròn lượng giác nằm phía trên trục hoành, xác định điểm M(x0; y0) sao cho 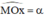
Khi đó ta có:
sin α = y0
cos α = x0
tan α = y0 / x0
cot α = x0 / y0
b) Gọi E, F là hình chiếu của M trên Oy, Ox.
Khi α < 90º thì x0 > 0, y0 > 0

\(0< a< \dfrac{\pi}{2}\Rightarrow0< \dfrac{a}{2}< \dfrac{\pi}{4}\Rightarrow sin\dfrac{a}{2}>0\)
\(\Rightarrow sin\dfrac{a}{2}=\sqrt{1-cos^2\dfrac{a}{2}}=\dfrac{3}{5}\)
\(sina=2sin\dfrac{a}{2}cos\dfrac{a}{2}=2.\left(\dfrac{4}{5}\right)\left(\dfrac{3}{5}\right)=\dfrac{24}{25}\)
\(cosa=\pm\sqrt{1-sin^2a}=\pm\dfrac{7}{25}\)
\(tana=\dfrac{sina}{cosa}=\pm\dfrac{24}{7}\)

`0<α<π/2 => {(sinα>0),(cosα>0):}`
`tanα+cotα=2`
Mà `tanα.cotα=1`
`=>` \(\left\{{}\begin{matrix}tan\text{α}=1\\cot\text{α}=1\end{matrix}\right.\)
`=> α=π/4`
`=> sinα=cosα=\sqrt2/2`


a) Do MN song song với Ox nên \(\alpha = \widehat {OMN} = \widehat {ONM} = \widehat {NOx'}\)
Mà \(\widehat {xON} = {180^o} - \widehat {NOx'} = {180^o} - \alpha \)
\( \Rightarrow \widehat {xON} = {180^o} - \alpha \)
b) Dễ thấy: Điểm N đối xứng với M qua trục Oy
\( \Rightarrow N( - {x_0};{y_0})\)
Lại có: điểm N biểu diễn góc \({180^o} - \alpha \)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = {y_N} = {y_0}\\\cos ({180^o} - \alpha ) = {x_N} = - {x_0}\end{array} \right.\);
Mà: \(\sin \alpha = {y_0};\;\cos \alpha = {x_0}\)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = \sin \alpha \;\\\cos ({180^o} - \alpha ) = - \cos \alpha \end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\tan ({180^o} - \alpha ) = - \tan \alpha \;\\\cot ({180^o} - \alpha ) = - \cot \alpha \end{array} \right.\)

a)\(\sin^2\alpha+\cos^2\alpha=1\Rightarrow\sin^2\alpha=1-\cos^2\alpha\)
\(\Rightarrow1-2^2=-3\) \(\Rightarrow\cos=-\sqrt{3}\left(0< \alpha< \dfrac{\pi}{2}\right)\)
b) \(\tan\alpha\times\cot\alpha=1\Rightarrow\tan\alpha=\dfrac{1}{\cot\alpha}\Rightarrow\tan=\dfrac{1}{4}\)
a)Do \(0< \alpha< \dfrac{\pi}{2}\) nên các giá trị lượng giác của \(\alpha\) đều dương.
\(cos\alpha=2sin\alpha\)(1)
Nếu \(sin\alpha=0\Rightarrow cos\alpha\) (vô lý).
Vì vậy \(sin\alpha\ne0\) . Từ (1) \(\Rightarrow\dfrac{cos\alpha}{sin\alpha}=2\)\(\Leftrightarrow cot\alpha=2\).
Suy ra: \(tan\alpha=\dfrac{1}{2}\).
\(sin\alpha=\sqrt{\dfrac{1}{1+cot^2\alpha}}=\dfrac{1}{\sqrt{3}}\).
\(cos\alpha=\sqrt{1-sin^2\alpha}=\sqrt{\dfrac{2}{3}}\).

a:
2: pi/2<a<pi
=>sin a>0 và cosa<0
tan a=-2
1+tan^2a=1/cos^2a=1+4=5
=>cos^2a=1/5
=>\(cosa=-\dfrac{1}{\sqrt{5}}\)
\(sina=\sqrt{1-\dfrac{1}{5}}=\dfrac{2}{\sqrt{5}}\)
cot a=1/tan a=-1/2
3: pi<a<3/2pi
=>cosa<0; sin a<0
1+cot^2a=1/sin^2a
=>1/sin^2a=1+9=10
=>sin^2a=1/10
=>\(sina=-\dfrac{1}{\sqrt{10}}\)
\(cosa=-\dfrac{3}{\sqrt{10}}\)
tan a=1:cota=1/3
b;
tan x=-2
=>sin x=-2*cosx
\(A=\dfrac{2\cdot sinx+cosx}{cosx-3sinx}\)
\(=\dfrac{-4cosx+cosx}{cosx+6cosx}=\dfrac{-3}{7}\)
2: tan x=-2
=>sin x=-2*cosx
\(B=\dfrac{-4cosx+3cosx}{-6cosx-2cosx}=\dfrac{1}{8}\)

\(\left\{{}\begin{matrix}tan\alpha=-\dfrac{7}{3}\\sin^2\alpha+cos^2\alpha=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{sin\alpha}{cos\alpha}=-\dfrac{7}{3}\\sin^2\alpha+cos^2\alpha=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin\alpha=-\dfrac{7}{3}cos\alpha\\sin^2\alpha+cos^2\alpha=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin\alpha=-\dfrac{7}{3}cos\alpha\\\dfrac{49}{9}cos^2\alpha+cos^2\alpha=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin\alpha=-\dfrac{7}{3}cos\alpha\\cos^2\alpha=\dfrac{9}{58}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin\alpha=-\dfrac{7}{3}cos\alpha\\cos\alpha=\dfrac{3}{\sqrt{58}}\end{matrix}\right.\) (Vì \(\dfrac{3\pi}{2}< \alpha< 2\pi\Rightarrow cos\alpha>0\))
\(\Leftrightarrow\left\{{}\begin{matrix}sin\alpha=-\dfrac{7}{\sqrt{58}}\\cos\alpha=\dfrac{3}{\sqrt{58}}\end{matrix}\right.\)
\(cot\alpha=\dfrac{1}{tan\alpha}=-\dfrac{3}{7}\)