Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Định lí Cô sin : Tam giác ABC có AB = c, BC = a, AC = c thì ta có :
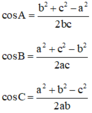

Định lí cosin: Trong tam giác ABC
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\quad (1)\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\quad (2)\\{c^2} = {b^2} + {a^2} - \,2ab.\cos C\quad (3)\end{array}\)
Ta có \((1) \Leftrightarrow 2bc\cos A = {b^2} + {c^2} - {a^2}\, \Leftrightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}\,}}{{2b\,c}}.\)
Tương tự từ (2) và (3) ta suy ra \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\); \(\cos C = \frac{{{b^2} + {a^2} - {c^2}\,}}{{2b\,a}}\)

TL:
sinA+sinB+sinC=1-cosA+cosB+cosC => Tam giác ABC Vuông tại A
Vế trái = sinA + sinB + sinC
= 2sin(A + B)/2.cos(A - B)/2 + 2sinC/2.cosC/2
= 2cosC/2.cos(A - B)/2 + 2sinC/2.cosC/2
= 2cosC/2[cos(A - B)/2 + sinC/2]
=2.cosC/2.[cos(A - B)/2 + cos(A + B)/2]
= 4.cosC/2.cosB/2.cosA/2
Vế phải = 1 - cosA + cosB + cosC
= 2sin²A/2 + 2cos(B + C)/2.cos(B - C)/2
= 2.sinA/2[sinA/2 + cos(B - C)/2] (vì cos(B + C)/2 = sinA/2)
= 2.sinA/2[cos(B + C)/2 + cos(B - C)/2
= 4.sinA/2.cosB/2.cosC/2
Vậy sinA + sinB + sinC = 1 - cosA + cosB + cosC
<=> cosA/2.cosB/2.cosC/2 = sinA/2.cosB/2.cosC/2
<=> cosB/2.cosC/2(sinA/2 - cosA/2) = 0
mà cosB/2 ≠ 0 và cosC/2 ≠ 0
=> sinA/2 = cosA/2
<=> A/2 = 45o
<=> A = 90o
tam giác ABC vuông tại A


Chọn B.
Ta có: góc A tù nên cos A < 0 ; sinA > 0 ; tan A < 0 ; cot A < 0
Do góc A tù nên góc B và C là các góc nhọn có các giá trị lượng giác đều dương
Do đó: M > 0 ; N > 0 ; P > 0 và Q < 0.

\(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
\(=\dfrac{b^2+c^2-a^2}{2abc}+\dfrac{a^2+c^2-b^2}{2abc}+\dfrac{a^2+b^2-c^2}{2abc}\)
\(=\dfrac{a^2+b^2+c^2}{2abc}\) (đpcm)
a2 = b2 + c2 - 2bc.cosA
b2 = a2 + c2 - 2ac.cosB
c2 = a2 + b2 - 2ab.cosC
⇒ a2 + b2 + c2 = 2bc.cosA + 2ac.cosB + 2ab.cosC
⇒ VT = \(\dfrac{2bc.cosA}{2abc}+\dfrac{2ab.cosC}{2abc}+\dfrac{2ac.cosB}{2abc}\)
⇒ VT = \(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)

P ⇒ Q: “ Nếu tam giác ABC có hai góc bằng 60o thì ABC là một tam giác đều”
Giả thiết: “Tam giác ABC có hai góc bằng 60o ”
Kết luận: “ABC là một tam giác đều”
Phát biểu lại định lí này dưới dạng điều kiện cần: “ABC là một tam giác đều là điều kiện cần để tam giác ABC có hai góc bằng 60o”
Phát biểu lại định lí này dưới dạng điều kiện đủ : “Tam giác ABC có hai góc bằng 60o là điều kiện đủ để ABC là tam giác đều”

Ta có : \(cos2A+2\sqrt{2}\left(cosB+cosC\right)=3\)
\(\Leftrightarrow1-2sin^2A+2\sqrt{2}.2.cos\left(\dfrac{B+C}{2}\right).cos\left(\dfrac{B-C}{2}\right)=3\)
\(\Leftrightarrow2sin^2A-4\sqrt{2}.sin\dfrac{A}{2}.cos\left(\dfrac{B-C}{2}\right)+2=0\)
\(\Leftrightarrow sin^2A-2\sqrt{2}.sin\dfrac{A}{2}.cos\left(\dfrac{B-C}{2}\right)+1=0\)
\(\Delta\) ABC không tù nên \(cos\dfrac{A}{2}\ge cos45^o=\dfrac{\sqrt{2}}{2}\)
Suy ra : VT \(\ge sin^2A-4.cos\dfrac{A}{2}.sin\dfrac{A}{2}.cos\left(\dfrac{B-C}{2}\right)+1=K\)
Thấy : \(K=sin^2A-2.sinA.cos\left(\dfrac{B-C}{2}\right)+cos\left(\dfrac{B-C}{2}\right)^2+1-cos\left(\dfrac{B-C}{2}\right)^2\)
\(=\left(sinA-cos\left(\dfrac{B-C}{2}\right)\right)^2+sin^2\left(\dfrac{B-C}{2}\right)\ge0\)
Suy ra : \(VT\ge K\ge0=VP\)
Dấu " = " xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}sinA=cos\left(\dfrac{B-C}{2}\right)\\sin\left(\dfrac{B-C}{2}\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sinA=cos0^o=1\\B=C\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A=\dfrac{\pi}{2}\\B=C=\dfrac{\pi}{4}\end{matrix}\right.\) ( do \(A+B+C=\pi\) )
Vậy ...
Định lí:
Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Ta có các hệ thức sau: a2 = b2 + c2 - 2bc.cosA (1)
b2 = a2 + c2 - 2bc.cosB (2)
c2 = a2 + b2 - 2bc.cosC (3)
Hệ quả: Từ định lí cosin suy ra:
cosA =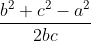 cosB =
cosB = 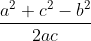
cosC =