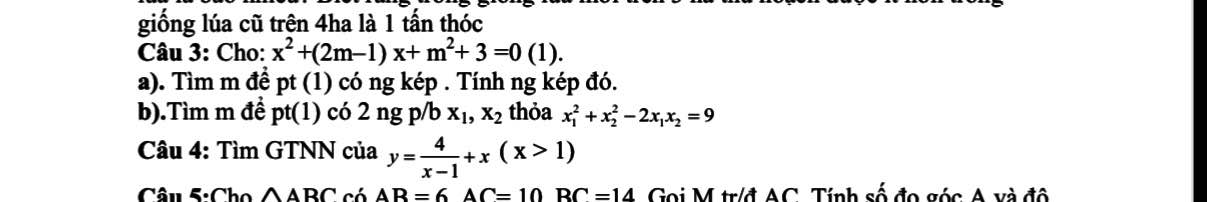K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 1 2022
Câu 3:
a: Để phương trình có nghiệm kép thì \(\left(2m-1\right)^2-4\left(m^2+3\right)=0\)
\(\Leftrightarrow4m^2-4m+1-4m^2-12=0\)
hay m=-11/4
15 tháng 6 2023
5:
(d) vuông góc 2x-y-2018=0
=>(d): x+2y+c=0
(C): x^2+4x+4+y^2-6y+9-25=0
=>(x+2)^2+(y-3)^2=25
=>R=5; I(-2;3)
Theo đề, ta có: d(I;(d))=5
=>\(\dfrac{\left|1\cdot\left(-2\right)+2\cdot3+c\right|}{\sqrt{5}}=5\)
=>|c+4|=5căn 5
=>c=5căn5-4 hoặc c=-5căn 5-4
15 tháng 4 2023
Số hạng chứa x^15 sẽ là \(\left(a+b\right)x^{15}\), với a là hệ số của x^10 trong (3x+4)^10, b là hệ số của x^5 trong (2x-1)^5
(3x+4)^10
SHTQ là: \(C^k_{10}\cdot\left(3x\right)^{10-k}\cdot4^k=C^k_{10}\cdot3^{10-k}\cdot4^k\cdot x^{10-k}\)
số hạng chứa x^10 tương ứng với 10-k=10
=>k=0
=>\(a=C^0_{10}\cdot3^{10}\cdot4^0=59049\)
(2x-1)^5
SHTQ là: \(C^k_5\cdot\left(2x\right)^{5-k}\cdot\left(-1\right)^k=C^k_5\cdot2^{5-k}\cdot\left(-1\right)^k\cdot x^{5-k}\)
SH chứa x^5 tương ứng với 5-k=5
=>k=0
=>\(b=C^0_5\cdot2^5\cdot\left(-1\right)^0=32\)
=>Số cần tìm là 59081x15
ES
2
HN
26 tháng 8 2021
Sai thì thôi nha :>
Theo đề ra: ABCD là hình bình hành
\(vectoAD+vectoAB=vectoAC\) và \(vectoAB+vectoAC=vectoBD\)
\(\Leftrightarrow vectoAD=-vectoAB+vectoAC\)
\(\Leftrightarrow vectoAD=vectoAB+vectoAC-2vectoAB=vectoBD-2vectoAB=b-2a\)
DD
Đoàn Đức Hà
Giáo viên
27 tháng 8 2021
\(\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{AB}+\overrightarrow{AD}\)
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
suy ra \(2\overrightarrow{AD}=\overrightarrow{BD}+\overrightarrow{AC}\Leftrightarrow\overrightarrow{AD}=\frac{\overrightarrow{BD}+\overrightarrow{AC}}{2}=\frac{a+b}{2}\).
3 tháng 8 2016
Gọi đàn thiên nga là x , ta có :
x + \(\frac{1}{2}\) x + 2 = 200
x + \(\frac{1}{2}\) x = 200 - 2 = 198
x . ( 1 + \(\frac{1}{2}\) ) = 198
x . \(\frac{3}{2}\) = 198
x = 198 : \(\frac{3}{2}\)
x = 132
Vậy đàn thiên nga có 132 con