Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
+) x2 +2x + 1
f(-1) = (-1)2 + 2. (-1) + 1 = 1 + (-2) +1 = 0
f(1) = 12 +2 . 1 + 1 = 4
f(0) = 02 + 2.0 +1 = 1
b) y = 1
=> 1 = x2 + 2x + 1
=> x2 + 2x = 0
=> x . x + 2x = 0
=> x . ( x+2) = 0
=> x+ 2 = 0
=> x = -2

ta có hàm số y = f(x) = 3x2 + 5
vì x2 \(\ge\)0 \(\forall\)x \(\Rightarrow\)3x2 + 5 \(\ge\)5 hay y \(\ge\)5
Vậy với mọi giá trị của x thì hàm số đã cho luôn nhận giá trị dương
Vì x2>0 ( với mọi x ) nên 3x2+5 > 0
Vậy f(x) = 3x2 + 5 luôn nhận giá trị dương với mọi giá trị x ( đpcm ).
XONG RỒI ĐÓ...

Ta có : \(f\left(x\right)=x^2+2x+1=\left(x+1\right)^2\)
a, \(f\left(1\right)=\left(1+1\right)^2=2^2=4\)
\(f\left(0\right)=\left(0+1\right)^2=1^2=1\)
b, Ta có : y = 1 hay \(f\left(x\right)=1\)
\(\Leftrightarrow\left(x+1\right)^2=1\Leftrightarrow x^2+2x+1=1\)
\(\Leftrightarrow x^2+2x=0\Leftrightarrow x\left(x+2\right)=0\Leftrightarrow x=0;-2\)
Vậy \(x=\left\{0;-2\right\}\)

Với mọi \(x\in R\) , ta có \(3x^2\ge0\) suy ra \(3x^2+5>5\). Vì vậy với mọi giá trị x thì hàm số đã cho nhận giá trị dương.

Điền giá trị y = f(x) vào bảng sau:
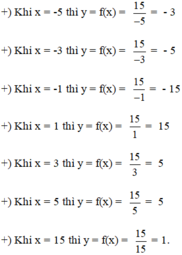
| x | -5 | -3 | -1 | 1 | 3 | 5 | 15 |
| y=f(x) | -3 | -5 | -15 | 15 | 5 | 3 | 1 |

Ta có: f(1) = 2.12 – 5 = 2 – 5 = -3
f(-2) = 2.(-2)2 – 5 = 8 – 5 = 3
f(0) = 2.02 – 5 = 0 – 5 = -5
f(2) = 2.22 – 5 = 2.4 – 5 = 3
ok, bn...đáp án là... mk éo bt làm :))
@Khuê =)) vậy là bn ''gà'' hơn mk rồi.
\(f\left(x\right)=7\)hay \(9x^2-2=7\)
\(\Leftrightarrow9x^2=9\Leftrightarrow x^2=1\Leftrightarrow x=\pm1\)
\(f\left(x\right)=1\)hay \(9x^2-2=1\Leftrightarrow x^2=\frac{1}{3}\Leftrightarrow x=\pm\sqrt{\frac{1}{3}}\)