Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
Δ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 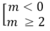

Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
∆ ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 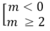

Chọn D
Ta có: y ' = 3 x 2 - 4 x , y ' ' = 6 x - 4 ;
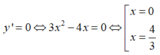
y''(0) = -4 < 0; y''(4/3) = 4 > 0. Do đó hàm số có hai cực trị là x = 0 và x = 4/3
Các mệnh đề (1); (2) và (3) sai;mệnh đề (4) đúng.

Đáp án: A.
Hàm số nghịch biến trên từng khoảng ( - ∞ ; -m), (-m; + ∞ ) khi và chỉ khi
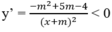
⇔ - m 2 + 5m - 4 < 0
⇔ 

Đáp án: A.
Hàm số nghịch biến trên từng khoảng (- ∞ ; -m), (-m; + ∞ ) khi và chỉ khi
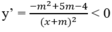
⇔ - m 2 + 5m - 4 < 0
⇔ ![]()

Gọi \(S_n\) là cách thỏa ycđp
Muốn lên và xuống thang n bậc \(\left(n>3\right)\) có 3 cách :
- Bước tới bậc n-1 rồi bước 1 bậc để lên n và xuống 1 bậc: 1 cách.
- Bước tới bậc n-2 rồi bước 2 bậc để lên n, sau đó xuống 2 bậc hoặc bước lên tửng bậc, xuống từng bậc hoặc xuống 2 bậc: 3 cách.
- Bước tới bậc n-3 để lên n rồi xuống thang: 9 cách (lấy theo VD cho nhanh).
Ta có hệ thức truy hồi, với \(n>3\)3
\(S_n=S_{n-1}+S_{n-2}+S_{n-3}\)
Khởi tạo : \(S_1=1,S_2=3,S_3=9\)
Suy ra : \(S_{11}=157+289+531=977\) cách .

Chọn C.
Ta có ![]()
![]()
![]()
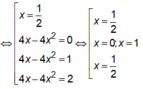
Do đó hàm số y = f ( 4 x - 4 x 2 ) có ba điểm cực trị là 0; 1 2 ;1
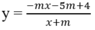
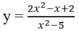


Chọn C
Hàm số bậc ba: y = a x 3 + b x 2 + c x + d , ( a # 0 )
Nếu ∆ ' ≤ 0 thì y ' không đổi dấu trên R nên hàm số không có cực trị.
Nếu ∆ ' > 0 thì phương trình y ' = 0 luôn có hai nghiệm phân biệt x 1 , x 2 và y ' đổi dấu khi x chạy qua x 1 , x 2 nên hàm số đạt cực trị tại x 1 , x 2