Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc xe 1 là x
=>vận tốc xe 2 là x+20
Theo đề, ta có: 4x=3(x+20)
=>4x=3x+60
=>x=60
=>Vận tốc xe 2 là 80km/h
AB=4*60=240(km)

Gọi thời gian xe thứ nhất đi hết quãng đường AB là a.
Thời gian xe thứ hai đi hết quãng đường AB là b.
\(60\%=\frac{3}{5}\)
Ta có: \(\frac{a}{b}=\frac{5}{3}\Rightarrow\frac{a}{5}=\frac{b}{3}\) và \(a-b=4\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{5}=\frac{b}{3}=\frac{a-b}{5-3}=\frac{4}{2}=2\)
Suy ra:
\(\frac{a}{5}=2\Rightarrow a=10\)
\(\frac{b}{3}=2\Rightarrow b=6\)

1 giờ xe thứ nhất đi được: 1 : 4 = 1/4 (quãng đường)
1 giờ xe thứ hai đi được: 1 : 5 = 1/5 (quãng đường)
8km ứng với: 1/4 - 1/5 = 1/20 (quãng đường)
Quãng đường dài: 8 : 1/20 = 160 (km)
Vận tốc của xe thứ nhất là: 160 : 4 = 40 (km/h)
Vận tốc của xe thứ hai là: 160 : 5 = 32 (km/h)

Ta có: 1 giờ 20 phút = 80 phút
1 giờ 30 phút = 90 phút
Gọi V1, V2 (m/ phút) lần lượt là vận tốc của xe đi 80 phút và 90 phút.
Vì quãng đường không đổi nên vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên:
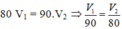
Do trong 1 phút xe thứ nhất đi hơn xe thứ hai 100m nên: V1 - V2 = 100
Theo tính chất dãy tỉ số bằng nhau ta có:
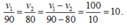
V1/90 = 10 ⇒ V1 = 10.90 = 900
V2/80 = 10⇒ V2 = 10.80 = 800
Vậy vận tốc xe thứ nhất V1 = 900(m/phút) = 54(km/h)
Vận tốc xe thứ hai V2 = 800(m/phút) = 48(km/h)

SỬa đề: Xe thứ ba đi chậm hơn xe thứ nhất 1h
Gọi vận tốc xe 1,2,3 lần lượt là a,b,c
Theo đề, ta có: 10a=5b=9c
=>a/9=b/18=c/10
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{9}=\dfrac{b}{18}=\dfrac{c}{10}=\dfrac{b-c}{18-10}=\dfrac{60}{8}=7,5\)
=>a=67,5; b=135, c=75
thời gian xe thứ hai đi là:
4,8:1,6=3(h)