Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Vì hai dao động cùng tần số cùng pha nên tỉ số động năng bằng tỉ số thế năng bằng tỉ số cơ năng:
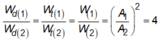
Khi W d ( 1 ) = 0,6 (J) thì
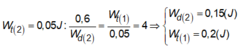
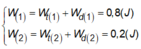
![]()
Suy ra:
![]()

Đáp án D
+ Vì hai dao động là luôn cùng pha nên ta có
0 , 72 1 2 k 3 A 2 = 1 2 k A 2 - 0 , 24 1 2 k A 2
⇒ E 2 = 1 2 k A 2 = 0 , 32 J
-> Khi thế năng của con lắc thứ nhất là 0,09 J thì:
9 E 1 - 0 , 09 9 E 1 = W d 2 E 1 ⇒ W d 2 = 0 , 31 J .

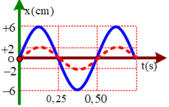
Dao động tổng hợp x = x1 + x2
+ Khi x2 = 0 thì x1 = x - x2 = \(-5\sqrt{3}\)
+ Khi x1 = - 5 thì x2 = x - x1 = -2 + 5 = 3
Giả sử pt \(x_1=10\cos\left(\omega t\right)\) thì \(x_2=A_2\cos\left(\omega t+\varphi\right)\) (với \(\left|\varphi\right|<\frac{\pi}{2}\))
Theo giả thiết ta có:
\(\begin{cases}10\cos\left(\omega t\right)=-5\sqrt{3}\\A_2\cos\left(\omega t+\varphi\right)=0\end{cases}\)\(\Rightarrow\begin{cases}\cos\left(\omega t\right)=-\frac{\sqrt{3}}{2}\\\cos\left(\omega t+\varphi\right)=0\end{cases}\)
cos O M1 M2 -√3/2 60°
Do \(\left|\varphi\right|<\frac{\pi}{2}\) nên ta chỉ có trường hợp như hình trên thỏa mãn, nghĩa là ta tìm đc \(\varphi=-\frac{\pi}{3}\)
Mặt khác: \(\begin{cases}10\cos\left(\omega t'\right)=-5\\A_2\cos\left(\omega t'+\varphi\right)=3\end{cases}\)\(\Rightarrow\begin{cases}\cos\left(\omega t'\right)=-\frac{1}{2}\\\cos\left(\omega t'+\varphi\right)=\frac{3}{A_2}\end{cases}\)
Cũng biểu diễn trên đường tròn lượng giác như trên, ta được
cos O M1 M2 -1/2 1/2
\(\Rightarrow A_2=6cm\)
Biên độ tổng hợp:
\(A^2=10^2+6^2+2.10.6.\cos\frac{\pi}{3}\Rightarrow A=14\)cm.
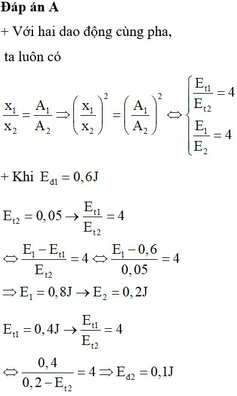
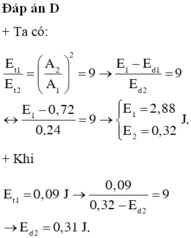



Đáp án A
Với hai dao động ngược pha, ta luôn có
→ Khi dao động 1 có động năng
thì