Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

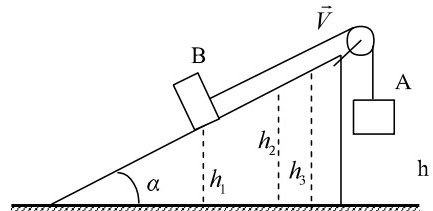
Chọn gốc thế năng tại mặt đất.
Cơ năng vật khi thả:
\(W=m_A\cdot gh+m_B\cdot gh=0,3\cdot10\cdot0,5+0,2\cdot10\cdot0,5=2,5J\)
Cơ năng khi vật A chạm đất:
\(W=\dfrac{1}{2}m_Av_A^2+\dfrac{1}{2}m_B\cdot v_B^2+m_B\cdot gh_2\)
Bảo toàn cơ năng:
\(v_A=v_B=\sqrt{\dfrac{2gh\cdot\left(m_A-m_B\cdot sin\alpha\right)}{m_A+m_B}}=2\)m/s
Em tham khảo nhé!!!

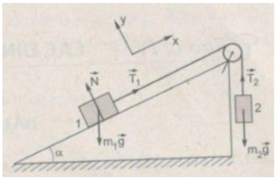
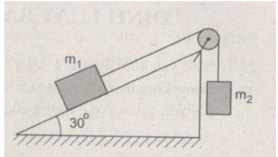
Chọn chiều dương của hệ tọa độ cho mỗi vật như hình vẽ
Xét vật 1:
Oy: N – m 1 gcos α = 0
Ox: T 1 – m 1 gsin α = m 1 a (1)
Xét vật 2:
M m 2 g – T 2 = m 2 a (2)
T 1 = T 2 = T (3)
Từ (1), (2) và (3) suy ra:
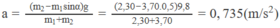
a > 0: vật m 2 đi xuống và vật m 1 đi lên.

Chọn A.

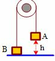
Chọn chiều dương là chiều chuyển động như hình vẽ.
Xét hệ (m1 + m2) thì T1 và T2 là nội lực, chỉ hai thành phần của ngoại lực là P2 và P 1 sin α là có tác dụng làm cho hệ chuyển động cùng một gia tốc và có độ lớn:
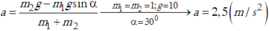
Xét riêng vật m2:
![]()

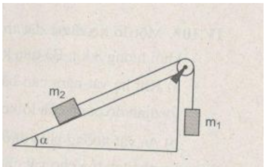
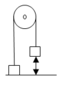
Hệ hai vật m 1 và m 2 chuyển động trong trọng trường, chỉ chịu tác dụng của trọng lực, nên cơ năng của hệ vật bảo toàn.
Vật m 1 , có trọng lượng P 1 = m 1 g ≈ 20 N và vật m2 có trọng lượng P 2 = m 2 g ≈ 1.10 = 10 N. Vì sợi dây nối hai vật này không dãn và P 1 > P 2 , nên vật m 1 chuyển động, thẳng đứng đi xuống và vật m 2 bị kéo trượt lên phía đỉnh mặt nghiêng với cùng đoạn đường đi và vận tốc. Như vậy, khi vật m 1 đi xuống một đoạn h thì thế năng của nó giảm một lượng W t 1 = m 1 gh, đồng thời vật m 2 cũng trượt lên phía đỉnh mặt nghiêng một đoạn h nên độ cao của nó tăng thêm một lượng hsinα và thế năng cũng tăng một lượng W t 2 = m 2 gh.
Theo định luật bảo toàn cơ năng, độ tăng động năng của hệ vật chuyển động trong trọng trường bằng độ giảm thế năng của hệ vật đó, tức là :
∆ W đ = - ∆ W t
⇒ 1/2( m 1 + m 2 ) v 2 = m 1 gh - m 2 gh.sin α
Suy ra W đ = 1/2( m 1 + m 2 ) v 2 = gh( m 1 - m 2 sin 30 ° )
Thay số, ta tìm được động năng của hệ vật khi vật m 1 đi xuống phía dưới một đoạn h = 50 cm :
W đ = 10.50. 10 - 2 .(2 - 1.0,5) = 7,5 J

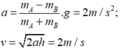
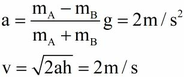
Tới "b " là câu hỏi nha mọi người em quên xuống hàng
bảo toàn cơ năng là ra bạn :D