Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4 cm = 40 mm; 5 cm = 50 mm; 6 cm = 60 mm
Ta có: \(\frac{40}{8}=\frac{50}{10}=\frac{60}{12}\)
=> Tam giác ABC đồng dạng tam giác A'B'C'

a) Hai tam giác đồng dạng với nhau vì \(\dfrac{40}{8}=\dfrac{50}{10}=\dfrac{60}{12}\) (cùng bằng 5)
b) Hai tam giác không đồng dạng với nhau vì \(\dfrac{3}{9}\ne\dfrac{4}{15}\)
c) Hai tam giác đồng dạng với nhau vì \(\dfrac{1}{2}=\dfrac{1}{2}=\dfrac{0,5}{1}\)

Lời giải:
a) Ta thấy:
$\frac{4}{8}=\frac{5}{10}=\frac{6}{12}$ nên 2 tam giác đồng dạng theo TH c.c.c
b) Pitago: $A'C'=\sqrt{B'C'^2-A'B'^2}=\sqrt{16^2-9^2}=5\sqrt{7}$
Xét tam giác $ABC$ và $A'B'C'$ có:
$\widehat{A}=\widehat{A'}=90^0$
$\frac{AB}{AC}\neq \frac{A'B'}{A'C'}$
Do đó 2 tam giác không đồng dạng

a) Ta có: \(\frac{4}{8}=\frac{5}{10}=\frac{6}{12}\left(=\frac{1}{2}\right)\)
hay \(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}\)
\(\Rightarrow\)\(\Delta A'B'C'~\Delta ABC\)
b) \(\Delta A'B'C'~\Delta ABC\)
\(\Rightarrow\)\(\frac{P_{A'B'C'}}{P_{ABC}}=\frac{A'B'}{AB}=\frac{8}{4}=2\)
Xin chào các bạn !!!
Hãy Đăng Kí Cho Channel Kaito1412_TV Để nhé !
Link là : https://www.youtube.com/channel/UCqgS-egZEJIX-ON873XpD_Q/videos?view_as=subscriber

Ta có: 3/9 = 6/18 ≠ 4/15 . Vậy hai tam giác đó không đồng dạng.

Sắp xếp các cạnh của mỗi tam giác theo thứ tự tăng dần rồi mới lập tỉ số, ta được hai tam giác đã cho đồng dạng.
b) Đặt 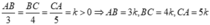
Đặt 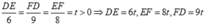
Lập tỉ số các cặp cạnh tương ứng, dẫn tới kết luận hai tam giác không đồng dạng.
Ta có: 4/8 = 5/10 = 6/12 .Vậy hai tam giác đó đồng dạng