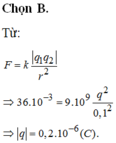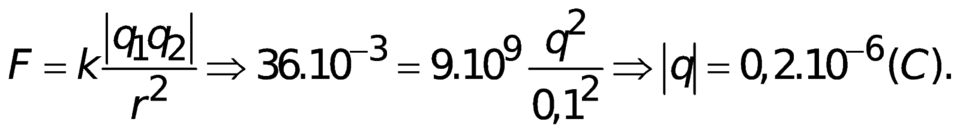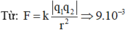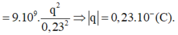Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(F=k.\dfrac{\left|q.q\right|}{r^2}\)
\(\Leftrightarrow q=\sqrt{\dfrac{F.r^2}{k}}=\sqrt{\dfrac{9.10^{-3}.\left(10.10^{-2}\right)^2}{9.10^9}}=\pm10^{-7}\left(C\right)\)

Gọi q1,q2 là điện tích của quả cầu 1 và quả cầu 2 trước khi chúng tiếp xúc với nhau.Độ lớn của lực tương tác giữa chúng được xác định theo định luật Culông :
\(F_1=k\frac{\left|q_1q_2\right|}{r^2}\) từ đó \(q_1q_2=-\frac{F_1r^2}{k}\) (có dấu \(\text{"−"}\) vì hai điên tích \(q_1,q_2\) trái dấu)
Thay số ta được : \(q_1q_2=-\frac{6,4}{9}.10^{-13}\left(1\right)\)
Sau khi tiếp xúc với nhau, điện tích của hai quả cầu trở nên bằng nhau và có độ lớn bằng \(\frac{\left|q_1+q_2\right|}{2}\) do đó lực đẩy giữa chúng là: \(F_2=\frac{k\left(\frac{q_1+q_2}{2}\right)^2}{r^2}\)
Suy ra \(\left(q_1+q_2\right)^2=\frac{4F_2r^2}{k}\) Thay số vào ta được \(\left(q_1+q_2\right)^2=16.10^{-14}\)
hay : \(q_1+q_2=\pm4.10^{-7}\left(2\right)\)
Giải hệ phương trình (1),(2) ta được :
\(q_1=-\frac{4}{3}.10^{-7}\approx-1,33.10^{-7}C\)
\(q_2=\frac{16}{3}.10^{-7}\approx5,33.10^{-7}C\)
hoặc \(q_1=\frac{4}{3}.10^{-7}\approx1,33.10^{-7}C\)
\(q_2=-\frac{16}{3}.10^{-7}\approx-5,33.10^{-7}C\)

F = k q 1 q 2 r 2 ⇒ 36.10 − 3 = 9.10 9 q 2 0 , 1 2 ⇒ | q | = 0 , 2.10 − 6 ( C )

Chọn B.
F = k q 1 q 2 r 2 ⇒ 9.10 − 3 = 9.10 9 ⋅ q 2 0 , 23 2 ⇒ | q | = 0 , 23.10 − ( C )

đáp án B
F = k q 1 q 2 r 2 = 9 . 10 - 3 = 9 . 10 9 q 2 0 , 23 2 ⇒ q = 0 , 23 . 10 - 6 C