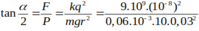Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

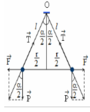
Góc lệch \(\alpha\) của dây treo được xác định bằng hệ thức (suy từ điều kiện cân bằng của hai quả cầu :)
\(\tan\alpha=\frac{F_đ}{P}\)
Với \(F_đ=k\frac{q^2}{a^2}\) Như vậy \(\tan\alpha=\frac{kq^2}{mga^2}\)
Thay số ta được : \(\tan\alpha=1\) suy ra \(\alpha=45^o\)
mình chưa hiểu đoạn tan a = F/P lắm bạn giải thích lại hộ mình đc ko


Sau khi cho hai quả cầu tiếp xúc với nhau thì mỗi quả cầu sẽ mang điện tích:
\(q'=\dfrac{q+0}{2}=\dfrac{q}{2}\)
Lực tương tác giữa hai quả cầu là lực điện: \(F=k.\dfrac{\left|q'\right|.\left|q'\right|}{r^2}=k.\dfrac{\left(\dfrac{q}{2}\right)^2}{2.sin\alpha.l}=k.\dfrac{\left(\dfrac{q}{2}\right)^2}{2.sin30^0}=k\left(\dfrac{q}{2}\right)^2\)
Xét một trong hai quả cầu (giả sử quả cầu nằm bên trái), ta có:
\(tan\alpha=\dfrac{F}{P}=\dfrac{k\left(\dfrac{q}{2}\right)^2}{mg}\)
\(\Rightarrow\left|q\right|=2\sqrt{\dfrac{tan\alpha.mg}{k}}=2\sqrt{\dfrac{tan30^0.5.10^{-3}.10}{9.10^9}}=3,58.10^{-6}C\)

a) Chiều lên phương của sợi dây:
\(T\cos a=P=mg\)
\(T\sin a=F\left(F=kq_1.\frac{q_2}{r^2}\right)\)
Mà hai quả nhiểm điên như nhau.
\(\Rightarrow q_1=q_2=q\Rightarrow F=mg.\tan a\)
a là góc lệch sợi dây phương ngang.
Có: \(\sin a=\frac{r}{\left(2l\right)}\)
Vì a rất nhỏ \(\Rightarrow\sin a=\tan a=\frac{3}{50}\)
Thay vào ra \(F=3,6.10^{-4}\Rightarrow q=1,2.10^{-8}C\)
b) Lúc này: \(F=\frac{k.q^2}{e.r^2}\)
Với e là hằng số điện mới.
\(\Rightarrow F=\frac{mg.q^2}{er^2}=mg.\tan a=mg.\sin a=\frac{mg.r'}{2l'}\)
Thay vào tính được r' = 20 cm