Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là vị trí tàu thu tín hiệu. Gọi \({t_A},{t_B}\) lần lượt là thời gian tín hiệu truyền từ trạm phát A,B đến M. Theo đề bài, ta có \({t_A} - {t_B} = - 0,0005s\).
Suy ra \(MA - MB = v.{t_A} - v.{t_B} = 292000.\left( { - 0,0005} \right) = - 146km\).
Gọi (H) là hyperbol ở dạng chính tắc nhận A,B làm hai tiêu điểm và đi qua M. Khi đó ta có:
\(\left\{ \begin{array}{l}2a = \left| {MA - MB} \right| = 146\\2c = AB = 300\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\c = 150\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\{b^2} = {c^2} - {a^2} = 17171\end{array} \right.\)
Vậy phương trình chính tắc của (H) là: \(\frac{{{x^2}}}{{5329}} - \frac{{{y^2}}}{{17171}} = 1\).

Chọn C.
Sau 2h quãng đường tàu thứ nhất chạy được là: S1 = 30.2 = 60km
Sau 2h quãng đường tàu thứ hai chạy được là: S2= 40.2 = 80 km
Suy ra sau 2h hai tàu cách nhau là:
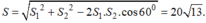

không hiểu nổi tại sao lại là 2 lần đường.
XA XB A B C : Lần gặp 1 c: lần gặp 2 xe XA còn qua đoạn CA nữa mới đủ 2 lần xe XB còn qua đoạn CB nữa mới đủ 2 lần tính đến lúc gặp nhau lần 2
Xin lỗi, vì khi cái này đăng lên, câu hỏi trên sẽ bị loại khỏi danh sách "chưa trả lời"

Sau 2h tàu thứ nhất ở vị trí B cách A là: \(2.30=60\left(km\right)\)
Tàu thứ 2 ở vị trí C cách A là: \(2.40=80\left(km\right)\)
Áp dụng định lý hàm cos:
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cos60^0}=20\sqrt{13}\approx72,1\left(km\right)\)

Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
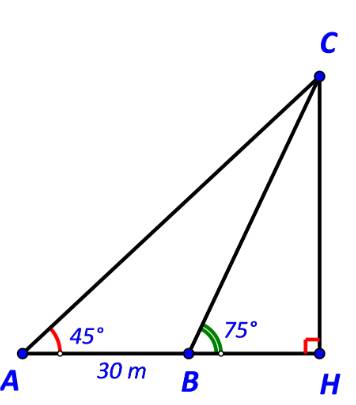
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)

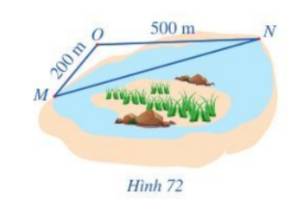
Áp dụng định lí cosin cho tam giác MON, ta có:
\(\begin{array}{l}M{N^2} = M{O^2} + O{N^2} - 2.OM.ON.\cos MON\\ \Rightarrow M{N^2} = {200^2} + {500^2} - 2.200.500.\cos {135^o}\\ \Rightarrow M{N^2} \approx 431421\\ \Rightarrow MN \approx 657\;(m)\end{array}\)
Bình phương hai vế ta được:
\(\begin{array}{l}{(8 - 40x)^2} + {(7 - 40x)^2} = 25\\ \Leftrightarrow 64 - 640x + 1600{x^2} + 49 - 560x + 1600{x^2} = 25\\ \Leftrightarrow 3200{x^2} - 1200x + 88 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{11}}{{40}}\\x = \frac{1}{{10}}\end{array} \right.\end{array}\)
Vậy phương trình có hai nghiệm là \(x = \frac{{11}}{{40}}\) và \(x = \frac{1}{{10}}\).