Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 3 giờ 45 phút = 3,75 giờ
Gọi vận tốc xe lửa thứ nhất là x (km/h) (x > 0)
Gọi vận tốc xe lửa thứ hai là y (km/h) (y >0)
Quãng đường xe lửa thứ nhất đi trong 10 giờ là: 10x (km)
Quãng đường xe lửa thứ hai đi trong 10 giờ là: 10y (km)
Vì hai xe đi ngược chiều và gặp nhau nên ta có pt: 10x + 10y = 750 (1)
Vì xe thứ nhất khởi hành trước xe thứ hai 3 giờ 45 phút nên khi gặp nhau thì thời gian xe thứ nhất đã đi là: 8 + 3,75 = 11,75 (giờ)
Quãng đường xe thứ nhất đã đi là: 11,75x (km)
Quãng đường xe thứ hai đã đi là: 8y (km)
Ta có pt: 11,75x + 8y = 750 (2)
Từ (1) và (2) ta có hệ pt: {10x+10y=75011,75x+8y=750⇔{x+y=7511,75x+8y=750{10x+10y=75011,75x+8y=750⇔{x+y=7511,75x+8y=750
⇔{8x+8y=60011,75x+8y=750⇔{−3,75x=−150x+y=75⇔{x=40y=35⇔{8x+8y=60011,75x+8y=750⇔{−3,75x=−150x+y=75⇔{x=40y=35
Đối chiếu với ĐK ta có x = 40; y = 35 đều thỏa mãn điều kiện
Vậy vận tốc xe thứ nhất là 40 km/h; Vận tốc xe lửa thứ hai là 35 km/h

Gọi x, y (km/h) lần lượt là vận tốc của xe thứ nhất và xe thứ hai. Điều kiện: x > 0, y > 0.
Vì hai xe khởi hành đồng thời và đi ngược chiều nhau, sau 10 giờ chúng gặp nhau nên ta có:
10x + 10y = 750
Vì xe thứ nhất khởi hành trước xe thứ hai 3 giờ 45 phút thì sau khi xe thứ hai đi được 8 giờ chúng gặp nhau nên thời gian xe thứ nhất đi được là:
3 giờ 45 phút + 8 giờ = 11 giờ 45 phút = 11(3/4) = 47/4 giờ
Ta có phương trình: (47/4)x + 8y = 750
Ta có hệ phương trình:
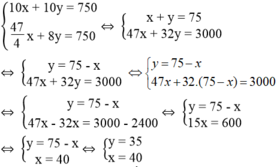
Giá trị của x và y thỏa điều kiện bài toán.
Vậy vận tốc của xe thứ nhất là 40 km/h, vận tốc của xe thứ hai là 35 km/h.

Gọi vận tốc xe t1 là x (x>0) (km/h)
vận tốc xe t2 là y (y>0) (km/h)
Hai xe khởi hành cùng lúc và đi ngược chiều nhau,sau 10h thì gặp ,ta có pt: \(10x+10y=750\left(1\right)\)
Xe 1 khởi hành trc xe 2 3h45p,xe 2 đi đc 8h thì gặp thì khi gặp nhau xe 1 đi được 11h45p = 47/4h
Ta có pt: \(\frac{47}{4}x+8y=750\left(2\right)\)
từ (1) và (2), ta có hệ: \(\hept{\begin{cases}10x+10y=750\\\frac{47}{4}x+8y=750\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=75\\47x+32y=3000\end{cases}}}\)
Giải hệ ta đc: x=40,y=35 (TMĐK)
Vậy...

xe lửa đi từ a vận tốc là : 35km
xe lửa đi từ b vận tốc là : 30 km

Bạn tích dùng cho mình đi không biết mình có giải đúng không nếu bạn cho là mình làm đúng thì tích đi mình sẽ giải ngay sau đó

gọi xe oto 1 và 2 lần lượt là x,y ( km/h, x và y lớn hơn 0 )
vì Hai xe ô tô ở hai địa điểm cách nhau một quãng đường 900 km ta có pt
10x + 10y = 900 (1)
vì nếu xe thứ nhất khởi hành trước xe thứ hai 9 giờ thì sau khi xe thứ hai đi được 6 giờ chúng gặp nhau ta có pt
15x + 6y =900 ( 2 )
từ 1 và 2 t có hpt
\(\Rightarrow\) còn lại bạn tự giải nhá

Tổng vận tốc của 2 xe là :
40 : 1 = 40 (km/h)
Chỉ làm đc thế thui vì mik mới lớp 6
Đổi 1 giờ=60 phút,
Thời gian xe A đi là: 60+27=87(phút)=1,5 giờ
Thời gian xe B đi là: 60-27=33(phút)=0,55 giờ
Vận tốc của xe A là: 40/1,45=27,59(km/giờ)
Vận tốc của xe B là: 40/0,55=72,72(km/giờ)
mk k chắc nữa, vì ms học lớp 6 thôi
Chúc bạn học tốt!^_^

Gọi x (km/h) là vận tốc của xe thứ nhất. Điều kiện: 0 < x < 90
Vì sau 1 giờ hai xe gặp nhau nên quãng đường hai xe đi được trong 1 giờ là 90km.
Suy ra tổng vận tốc của hai xe là 90km/h, vận tốc của xe thứ hai là 90 – x (km/h)
Quãng đường xe thứ nhất tiếp tục đi là 90 – x(km)
Thời gian xe thứ nhất đi quãng đường còn lại là (90 - x)/x (giờ)
Quãng đường xe thứ hai tiếp tục đi là x (km)
Thời gian xe thứ hai đi quãng đường còn lại là x/(90 - x) (giờ)
Xe thứ hai tới Hà Nội trước xe thứ nhất tới Nam Định là 27 phút bằng 9/20 (giờ)
Theo đề bài, ta có phương trình:
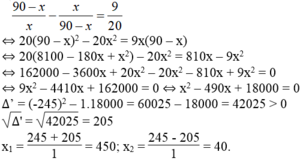
Giá trị x = 450 không thỏa mãn điều kiện bài toán.
Vậy vận tốc của xe thứ nhất là 40km/h
vận tốc của xe thứ hai là 90 – 40 = 50 km/h

Đổi 2h40ph=8/3 giờ
Gọi vận tốc xe thứ nhất là x (km/h), vận tốc xe thứ hai là y (km/h) với x;y>0
Do 2 xe đi ngược chiều gặp nhau sau 3 giờ nên: \(x+y=\dfrac{120}{3}=40\)
Quãng đường xe thứ nhất đi được sau 2h40ph: \(\dfrac{8x}{3}\) (km)
Quãng đường còn lại: \(120-\dfrac{8x}{3}\)
Do hai xe gặp nhau khi xe thứ 2 đi được 1 giờ nên:
\(x+y=\left(120-\dfrac{8x}{3}\right):1\Leftrightarrow\dfrac{11x}{3}+y=120\)
Ta được hệ: \(\left\{{}\begin{matrix}x+y=40\\\dfrac{11x}{3}+y=120\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=30\\y=10\end{matrix}\right.\)
