Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương trình dao động của một điểm M trên S 1 S 2 cách hai nguồn khoảng d 1 , d 2
là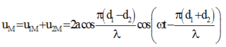 
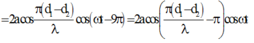
Sóng cùng pha với nguồn và có biên độ cực đại
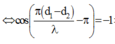
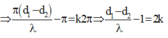
(với 
(không tính hai nguồn)). Ta được: 
có 8 giá
trị của k thảo mãn. Vậy có 8 điểm thỏa mãn yêu cầu bài toán.
Do có 9 điểm dao động cực đại kể cả nguồn
\(\Rightarrow l=8\cdot\dfrac{\lambda}{2}=4\lambda=40\\ \Rightarrow\lambda=10\left(cm\right)\)
\(\Rightarrow f=\dfrac{v}{\lambda}=\dfrac{60}{10}=6Hz\)
Chọn D
Đáp án C
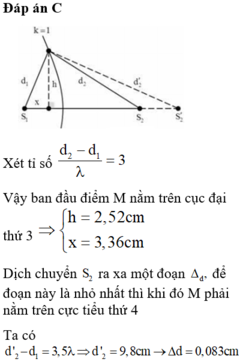
+ Xét tỉ số d 2 - d 1 λ = 3
Vậy ban đầu điểm M nằm trên cực đại thứ 3 ⇒ h = 2 , 52 cm x = 3 , 36 cm
Dịch chuyển S2 ra xa một đoạn ∆ d , để đoạn này là nhỏ nhất thì khi đó M phải nằm trên cực tiểu thứ 4
Ta có: d 2 ' - d 1 = 3 , 5 λ ⇒ d 2 ' = 9 , 8 cm → ∆ d = 0 , 83 cm .
Bước sóng \(\lambda=\frac{v}{f}=2cm\)
Số điểm dao động với biên độ cực tiểu ứng với số giá trị của k: \(-\frac{AB}{\lambda}-0,5\le k\le\frac{AB}{\lambda}-0,5\)
\(\Leftrightarrow-5,5\le k\le4,5\)
Suy ra có 10 giá trị của k, tức là có 10 điểm dao động với biên độ cực tiểu trên AB
Đáp án C
Đáp án: A
HD Giải: λ = v/f = 20/100 = 0,2cm
Hai nguồn cùng pha, số điểm dao động với biên độ cực đại trên AB, ta có:
-AB < kλ < AB
<=> -2 < 0,2k < 2
<=> - 10 < k < 10
Suy ra trên AB có 19 cực đại
Chọn đáp án A
Phương trình dao động của một điểm M trên S1S2 cách hai nguồn khoảng d1, d2 là:
u M = u 1 M + u 2 M = 2 a cos π d 1 − d 2 λ cos ω t − π d 1 + d 2 λ = 2 a cos π d 1 − d 2 λ cos ω t − 9 π = 2 a cos π d 1 − d 2 λ − π cos ω t
Sóng cùng pha với nguồn và có biên độ cực đại
⇔ cos π d 1 − d 2 λ − π = − 1 ⇒ π d 1 − d 2 λ − π = k 2 π ⇒ d 1 − d 2 λ − 1 = 2 k
(với − 9 λ < d 1 − d 2 < λ (không tính hai nguồn)).
Ta được: -5 < k < 4 ⇒ có 8 giá trị của k thỏa mãn.
Vậy có 8 điểm thỏa mãn yêu cầu bài toán.