Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Điều kiện để tại A có cực đại giao thoa là hiệu đường đi từ A đến hai nguồn sóng phải bằng số nguyên lần bước sóng: d 2 − d 1 = k λ ↔ l 2 + d 2 − l = k λ . (Với k = 1, 2, 3...)
Khi l càng lớn đường S 1 A cắt các cực đại giao thoa có bậc càng nhỏ (k càng bé), vậy ứng với giá trị lớn nhất của l để tại A có cực đại nghĩa là tại A đường S 1 A cắt cực đại bậc 1 (k = 1).
→ l 2 + 4 − l = 1 → l = 1,5 m . .

\(\lambda = v/f = 0,04m=4cm.\)
\(\triangle \varphi =0\)
Số điểm dao động cực đại trên đoạn thẳng đường kính 2R là:
\(-2R\leq d_2-d_1\leq 2R \Rightarrow -2R\leq (k+\frac{\triangle\varphi)}{2 \pi}\lambda\leq 2R \Rightarrow -2R \leq k.\lambda \leq 2R \\ \Rightarrow \frac{-2R}{\lambda}\leq k \leq \frac{2R}{\lambda} \Rightarrow -1,5 \leq k \leq 1,5 \Rightarrow k=-1,0,1\)
=> trên đường tròn bán kính R có 6 điểm dao động với biên độ cực đại.

Đáp án C
Điều kiện để tại A có cực đại giao thoa là hiệu đường đi từ A đến hai nguồn sóng phải bằng số nguyên lần bước sóng: d 2 - d 1 = k λ ↔ l 2 + d 2 - l = k λ . (Với k = 1, 2, 3...)
Khi l càng lớn đường S1A cắt các cực đại giao thoa có bậc càng nhỏ (k càng bé), vậy ứng với giá trị lớn nhất của l để tại A có cực đại nghĩa là tại A đường S1A cắt cực đại bậc 1 (k = 1).
l 2 + 4 - l = 1 → l = 1 , 5 m

chọn đáp án B
số điểm dao động với biên độ cực đại trên S 1 S 2 thoả mãn
-
S
1
S
2
λ
≤
k
≤
-
S
1
S
2
λ
⇒
-
5
,
5
≤
k
≤
5
,
5
A thuộc đường vuông góc với
S
1
S
2
qua
S
1
,để A gần
S
1
nhất dao động với biên độ cực đại thì A thuộc vân cực đại bậc -5
ta có
A
S
1
-
A
S
2
=
-
5
λ
A
S
1
2
+
S
1
S
2
2
=
A
S
2
2
L
2
+
S
1
S
2
2
=
(
L
+
2
)
2
⇒
L
=
0
.
21
m

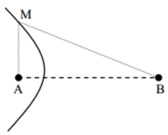
- Gọi d1, d2 là khoảng cách từ M đến 2 nguồn (M thuộc đường tròn và thỏa yêu cầu)
+ M thuộc đường tròn nên góc AMB là góc vuông
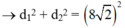
+ M dao động với biên độ cực đại nên: d1 - d2 = kλ
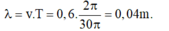
- Giải hệ phương trình trên ta được:
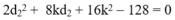
+ Chỉ có k = 0 là thỏa mãn ⇒ d1 = d2 = 8 cm
+ M dao động cùng pha với nguồn nên:
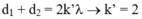
- Vậy có tất cả 2 điểm.

Bước sóng: \(\lambda = v.T=15.0,4=6cm\)
Ta có: \(d_2-d_1=15-21=-6cm=-\lambda\)
Suy ra M nằm trên vân giao thoa cực đại thứ 1.

Đáp án D
+ Bước sóng: λ = v/f = 40/20 = 20(cm)
+ Vì hai nguồn ngược pha và điểm M thuộc cực đại nên: MA – MB = (k + 0,5)λ
+ Điểm M gần A nhất khi M thuộc đường cực đại gần A nhất.
+ Số cực đại trên AB:
- AB λ - 1 2 < k < AB λ - 1 2
=> - 8,5 < k < 7,5 => điểm M thuộc k = - 8
=> MA – MB = -15 => MB = MA + 15 (1)
+ Trong tam giác vuông AMB ta có:
MB2 = MA2 + AB2 , từ (1) ta có (MA + 15)2 = MA2 + 162 => MA ≈ 1,033 cm .

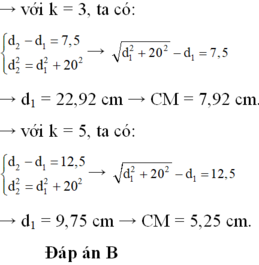
Đáp án D
Cách 1: vẽ hình ra: ta thấy ngay: để tại A là cực đại giao thoa, đồng thời đoạn d lớn nhất
thì A chính là giao của hypebol vân cực đại thứ nhất với đường thẳng vuông góc S 1 S 2 q u a S 1
Khi đó, ta có: A S 2 - A S 1 = 1 × λ ⇔ d 2 + 4 - d = 1
⇒ d = 1 , 5 m
Cách 2: dùng kiến thức hypebol
lập pt hệ trục tọa độ Oxy với O là trung điểm của S 1 S 2
khi đó, điểm A thuộc đường thẳng x = 1 và đồng thời thuộc hypebol vân cực đại thứ nhất.
pt hybpebol: x 2 a 2 - y 2 b 2 = 1
Trong đó:
a = λ 2 = 0 , 5 ; b 2 = c 2 - a 2 = O S 1 2 - a 2 = 1 2 - 0 , 5 2 = 0 , 75 ; x = 1 ; y = d
Như vậy, tính được ngay: d = 1,5 m.