Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi vận tốc của người xuất phát từ A là x, của người đi từ B là y (km/phút).
Điều kiện là x, y > 0.
Khi gặp nhau tại địa điểm C cách A là 2km :
Thời gian người xuất phát từ A đi đến C là: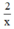 
(phút)
Thời gian người xuất phát từ B đi đến C là: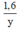 
(phút).
Vì hai người cùng xuất phát nên ta có phương trình:
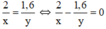
Mà nhận thấy trong cùng một thời gian, quãng đường người đi từ A đi được lớn hơn quãng đường người đi từ B đi được, do đó suy ra x > y.
Nếu cả hai cùng giữ nguyên vận tốc như trường hợp trên nhưng người đi chậm hơn (người đi từ B) xuất phát trước người kia 6 phút thì sẽ gặp nhau ở chính giữa quãng đường.
Khi đó, mỗi người đi được 1,8 km, Thời gian hai người đi lần lượt là: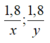 
Vậy ta có phương trình:
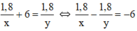
Ta có hệ phương trình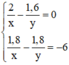 
Đặt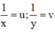 
, khi đó hệ phương trình trở thành:
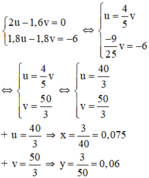
Vậy vận tốc của người đi từ A là 0,075 km/phút = 4,5 km/h;
vận tốc của người đi từ B là 0,06 km/phút = 3,6 km/h.
Gọi vận tốc của người xuất phát từ A là x, của người đi từ B là y (km/phút).
Điều kiện là x, y > 0.
Khi gặp nhau tại địa điểm C cách A là 2km :
Thời gian người xuất phát từ A đi đến C là: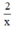 
(phút)
Thời gian người xuất phát từ B đi đến C là: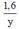 
(phút).
Vì hai người cùng xuất phát nên ta có phương trình:
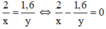
Mà nhận thấy trong cùng một thời gian, quãng đường người đi từ A đi được lớn hơn quãng đường người đi từ B đi được, do đó suy ra x > y.
Nếu cả hai cùng giữ nguyên vận tốc như trường hợp trên nhưng người đi chậm hơn (người đi từ B) xuất phát trước người kia 6 phút thì sẽ gặp nhau ở chính giữa quãng đường.
Khi đó, mỗi người đi được 1,8 km, Thời gian hai người đi lần lượt là: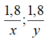 
Vậy ta có phương trình:
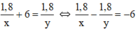
Ta có hệ phương trình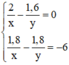 
Đặt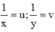 
, khi đó hệ phương trình trở thành:
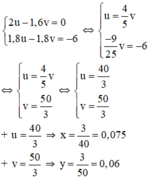
Vậy vận tốc của người đi từ A là 0,075 km/phút = 4,5 km/h;
vận tốc của người đi từ B là 0,06 km/phút = 3,6 km/h.
Gọi vận tốc của người xuất phát từ A là x, của người đi từ B là y (km/phút).
Điều kiện là x, y > 0.
Khi gặp nhau tại địa điểm C cách A là 2km :
Thời gian người xuất phát từ A đi đến C là \(\frac{2}{x}\)phút
Thời gian người xuất phát từ B đi đến C là \(\frac{1,6}{y}\)phút
Vì hai người cùng xuất phát nên ta có phương trình:
\(\frac{2}{x}=\frac{1,6}{y}\Leftrightarrow\frac{2}{x}-\frac{1,6}{y}=0\)
Mà nhận thấy trong cùng một thời gian, quãng đường người đi từ A đi được lớn hơn quãng đường người đi từ B đi được, do đó suy ra x > y.
Nếu cả hai cùng giữ nguyên vận tốc như trường hợp trên nhưng người đi chậm hơn (người đi từ B) xuất phát trước người kia 6 phút thì sẽ gặp nhau ở chính giữa quãng đường.
Khi đó, mỗi người đi được 1,8 km, Thời gian hai người đi lần lượt là: \(\frac{1,8}{x}:\frac{1,8}{y}\)
Vậy ta có PT :
\(\frac{1,8}{x}+6=\frac{1,8}{y}\Leftrightarrow\frac{1,8}{x}-\frac{1,8}{y}=-6\)
Ta có HPT \(\hept{\begin{cases}\frac{2}{x}-\frac{1,6}{y}=0\\\frac{1,8}{x}-\frac{1,8}{y}=-6\end{cases}}\)
Đặt \(\frac{1}{x}=u\); \(\frac{1}{y}=v\). Khi đó HPT chở thành :
\(\hept{\begin{cases}2u-1,6v=0\\1,8u-1,8v=-6\end{cases}\Leftrightarrow}\hept{\begin{cases}u=\frac{4}{5}v\\\frac{-9}{25}v=-6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}u=\frac{4}{5}v\\v=\frac{50}{3}\end{cases}\Leftrightarrow}\hept{\begin{cases}u=\frac{40}{3}\\v=\frac{50}{3}\end{cases}}\)
+ \(u=\frac{40}{3}\Rightarrow x=\frac{3}{40}=0,075\)
+ \(v=\frac{50}{2}\Rightarrow y=\frac{3}{50}=0,06\)
Vậy vận tốc của người đi từ A là 0,075 km/phút = 4,5 km/h
Vận tốc của người đi từ B là 0,06 km/phút = 3,6 km/h.
Giải bài toán bằng cách lập phwơng trình thôi bạn
Gọi vận tốc người đi từ A là Va ; người đi từ B là Vb ; Va > Vb vì người từ A đi nhanh hơn
Quãng đường người A đi : 2km ==> thời gian đi : 2/Va
Quãng đường người từ B đi : 3,6 - 2 = 1,6km ==> Thời gian : 1,6/Vb
Vì xuất phát cùng lúc nên thời gian đi bằng nhau ==> 2/Va = 1,6/Vb ==> Va / Vb = 2/1,6 = 5/4 (1)
* Người đi chậm là người đi từ B, quãng đường ng này đi trong 6p : Vb *(6/60) = Vb/10
Quãng đường người từ A đi đến khi gặp ở giữa đường : 1,8 ==> Thời gian đi : 1,8/Va cũng là thời gian người đi từ B sau 6p, vậy quãng đường người từ B đi được : Vb * (1,8/Va)
TA có : Vb * (1,8/Va) + Vb/10 = 1,8
==> 1,8*(Vb/Va) + Vb/10 = 1,8
Kết hợp (1) ==> 1,8*(4/5) + Vb/10 = 1,8
==> Vb/10 = 0,36
==> Vb = 3,6 km/h ; Va = 4.5km/h.
Cầu xin các bạn cho mình vài cái tick!!!!!
Giải bài toán bằng cách lập phwơng trình thôi bạn
Gọi vận tốc người đi từ A là Va ; người đi từ B là Vb ; Va > Vb vì người từ A đi nhanh hơn
Quãng đường người A đi : 2km ==> thời gian đi : 2/Va
Quãng đường người từ B đi : 3,6 - 2 = 1,6km ==> Thời gian : 1,6/Vb
Vì xuất phát cùng lúc nên thời gian đi bằng nhau ==> 2/Va = 1,6/Vb ==> Va / Vb = 2/1,6 = 5/4 (1)
* Người đi chậm là người đi từ B, quãng đường ng này đi trong 6p : Vb *(6/60) = Vb/10
Quãng đường người từ A đi đến khi gặp ở giữa đường : 1,8 ==> Thời gian đi : 1,8/Va cũng là thời gian người đi từ B sau 6p, vậy quãng đường người từ B đi được : Vb * (1,8/Va)
TA có : Vb * (1,8/Va) + Vb/10 = 1,8
==> 1,8*(Vb/Va) + Vb/10 = 1,8
Kết hợp (1) ==> 1,8*(4/5) + Vb/10 = 1,8
==> Vb/10 = 0,36
==> Vb = 3,6 km/h ; Va = 4.5km/h.
Gọi vận tốc của người thứ nhất là x(km/h), vận tốc của người thứ hai là y(km/h)
(Điều kiện: x>0 và y>0)
Thời gian để người thứ nhất đi được quãng đường từ A đến chỗ gặp là: \(\dfrac{2}{x}\left(h\right)\)
Thời gian để người thứ hai đi được quãng đường từ B đến chỗ gặp là: \(\dfrac{3,6-2}{y}=\dfrac{1.6}{y}\)
Vì hai người xuất phát cùng lúc nên ta có: \(\dfrac{2}{x}=\dfrac{1.6}{y}\)
=>1,6x=2y
=>x=1,25y
TH1: người thứ nhất đi chậm hơn
Thời gian người thứ nhất đi từ A đến chỗ gặp là: \(\dfrac{1.8}{x}\left(h\right)\)
Thời gian người thứ hai đi từ B đến chỗ gặp là \(\dfrac{1.8}{y}\left(h\right)\)
Vì người thứ nhất đi trước người thứ hai 6 phút=1/10h nên ta có:
\(\dfrac{1.8}{x}-\dfrac{1.8}{y}=\dfrac{1}{10}\)
=>\(\dfrac{1.8}{1,25y}-\dfrac{1.8}{y}=\dfrac{1}{10}\)
=>\(\dfrac{1}{y}\left(\dfrac{1.8}{1.25}-\dfrac{1.8}{1}\right)=\dfrac{1}{10}\)
=>\(\dfrac{1}{y}\cdot\dfrac{-9}{25}=\dfrac{1}{10}\)
=>\(\dfrac{1}{y}=\dfrac{1}{10}:\dfrac{-9}{25}=\dfrac{-1}{10}\cdot\dfrac{25}{9}=\dfrac{-25}{90}=-\dfrac{5}{18}\)(vô lý)
=>Loại
TH2: Người thứ hai đi chậm hơn
Thời gian người thứ nhất đi từ A đến chỗ gặp là: \(\dfrac{1.8}{x}\left(h\right)\)
Thời gian người thứ hai đi từ B đến chỗ gặp là \(\dfrac{1.8}{y}\left(h\right)\)
Vì người thứ hai đi trước người thứ nhất 6 phút nên ta có:
\(\dfrac{1.8}{y}-\dfrac{1.8}{x}=\dfrac{1}{10}\)
=>\(\dfrac{1.8}{y}-\dfrac{1.8}{1.25y}=\dfrac{1}{10}\)
=>\(\dfrac{1}{y}\left(1.8-\dfrac{1.8}{1.25}\right)=\dfrac{1}{10}\)
=>\(\dfrac{1}{y}\cdot\dfrac{9}{25}=\dfrac{1}{10}\)
=>\(\dfrac{1}{y}=\dfrac{1}{10}:\dfrac{9}{25}=\dfrac{1}{10}\cdot\dfrac{25}{9}=\dfrac{5}{9\cdot2}=\dfrac{5}{18}\)
=>\(y=\dfrac{18}{5}=3,6\left(nhận\right)\)
=>\(x=1,25\cdot y=1,25\cdot3,6=4,5\left(nhận\right)\)
vậy: vận tốc của người thứ nhất là 4,5km/h
vận tốc của người thứ hai là 3,6km/h
gọi vận tốc của 2 người lll : x, y(km/h) ĐK: x,y>0
trường hợp 1: có vận tốc, quãng đường => thời gian của mỗi người sẽ được tính như sau
thời gian người thứ nhất : 2/x (h) [thời gian=quãng đường: vận tốc]
thời gian người thứ hai : 3,6-2/y (h)
ta có phương trình : 2/x=1,6/y (h) (1)
trường hợp 2 : người đi chậm hơn xuất phát trước người kia 6 phút thì họ sẽ gặp nhau ở chính giữa quãng đường tức là thơi gian đi của 2 người như nhau hay bằng nhau
thời gian người thứ nhất đi sẽ đc tính 3,6:2/x (h)
thời gian người thứ hai đi sẽ đc tính 3,6:2/y (h)
vì là 1 người đi trc người kia 6' thì học gặp nhau nên ta có phương trình 1,8/y - 1,8/x = 1/10 (đổi 6'=1/10 giờ) (2)
từ (1) (2) ta có hpt {......
bạn giải hpt ra rồi xem thõa mãn đk k rồi kết luận...:)))
y (km/h) là vận tốc xe đi từ B-A
ĐK: x,y > 0
thời gian xe 1 đi từ A đến địa điểm cách A 2km: 2x(h)
thời gian xe 2 đi từ B đến điểm cách A 2km: 1,6y(h)
ta có pt : 2x=1,6y (1)
Nếu cả 2 cùng giữ nguyên vận tốc như ban đầu thì:
+ thời gian xe 2 đi được nửa quảng đường ( đã xuất phát trước 6p):
1,8y−0,1(h)
+ thời gian xe 1 đi được nửa quảng đường: 1,8x
Ta có pt: 1,8x=1,8y−0,1 (2)
Từ (1) và (2) ta có hệ pt :
⎧⎩⎨⎪⎪⎪⎪⎪⎪2x=1,6y1,8x=1,8y−0,1 ⇔⎧⎩⎨⎪⎪x=1,25y1,81,25y=1,8y−0,1 ⇔⎧⎩⎨⎪⎪x=1,25y0,36y=0,1 ⇔{x=1,25.3,6y=3,6 ⇔{x=4,5y=3,6 (TM)
Vậy vận tốc của xe 1 là 4,5 km/h vận tốc xe 2 là 3,6 km/h
Bài 2:
Trường hợp 1: a=0
Pt sẽ là -4x-3=0
hay x=-3/4
Trường hợp 2: a<>0
\(\text{Δ}=\left(-4\right)^2-4a\left(a-3\right)\)
\(=16-4a^2+12a=-4a^2+12a+16\)
\(=-4\left(a^2-3a-4\right)\)
\(=-4\left(a-4\right)\left(a+1\right)\)
Để phương trình có nghiệm thì -4(a-4)(a+1)>=0
=>(a-4)(a+1)<=0
=>-1<=a<=4
Gọi vận tốc của người xuất phát từ A là x, của người đi từ B là y (km/phút).
Điều kiện là x, y > 0.
Khi gặp nhau tại địa điểm C cách A là 2km :
Thời gian người xuất phát từ A đi đến C là: \(\dfrac{2}{x}\) ( phút)
Thời gian người xuất phát từ B đi đến C là: \(\dfrac{1,6}{y}\) (phút)
Vì hai người cùng xuất phát nên ta có phương trình:
\(\dfrac{2}{x}=\dfrac{1,6}{y}\Leftrightarrow\dfrac{2}{x}-\dfrac{1,6}{y}=0\)
Mà nhận thấy trong cùng một thời gian, quãng đường người đi từ A đi được lớn hơn quãng đường người đi từ B đi được, do đó suy ra x > y.
Nếu cả hai cùng giữ nguyên vận tốc như trường hợp trên nhưng người đi chậm hơn (người đi từ B) xuất phát trước người kia 6 phút thì sẽ gặp nhau ở chính giữa quãng đường.
Khi đó, mỗi người đi được 1,8 km, Thời gian hai người đi lần lượt là:
\(\dfrac{1,8}{x};\dfrac{1,8}{y}\)
Vậy ta có phương trình:
\(\dfrac{1,8}{x}+6=\dfrac{1,8}{y}\Leftrightarrow\dfrac{1,8}{x}-\dfrac{1,8}{y}=-6\)
ta có hệ pt:
\(\left\{{}\begin{matrix}\dfrac{2}{x}-\dfrac{1,6}{y}=0\\\dfrac{1,8}{x}-\dfrac{1,8}{y}=-6\end{matrix}\right.\)
Đặt \(\dfrac{1}{x}=u;\dfrac{1}{y}=v\) ; khi đó hệ phương trình trở thành:
\(\left\{{}\begin{matrix}2u-1,6v=0\\1,8u-1,8v-=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{4}{5}v\\-\dfrac{9}{25}v=-6\end{matrix}\right.\)
\(\left\{{}\begin{matrix}u=\dfrac{40}{3}\Rightarrow x=\dfrac{3}{40}=0,075\\v=\dfrac{50}{3}\Rightarrow y=\dfrac{3}{50}=0,06\end{matrix}\right.\)
Vậy vận tốc của người đi từ A là 0,075 km/phút = 4,5 km/h
vận tốc của người đi từ B là 0,06 km/phút = 3,6 km/h.
Sao thử lại k đúng