Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo bài: \(d_1=60cm,d_2=48cm\)
Áp dụng quy tăc momen lực:
\(F_1\cdot d_1=F_2\cdot d_2\) \(\Rightarrow F_1\cdot60=F_2\cdot48\)
\(\Rightarrow60F_1-48F_2=0\left(1\right)\)
Mà vật nặng 900N \(\Rightarrow F_1+F_2=900N\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) \(\Rightarrow\left\{{}\begin{matrix}F_1=400N\\F_2=500N\end{matrix}\right.\)
Chọn A

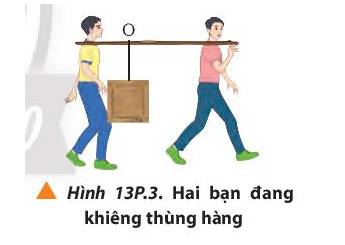
Tham khảo hình:
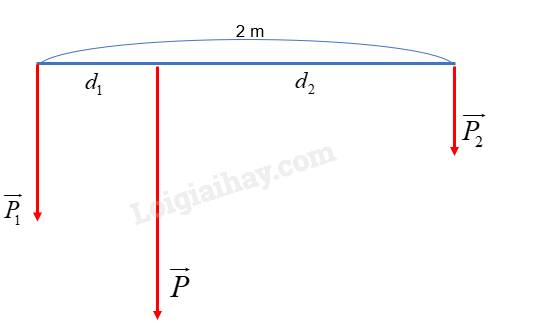
Theo bài ta có lực đè lên vai người đằng sau lớn hơn lực đè lên vai người đằng trước
=> P1 – P2 = 100 (1)
Mặt khác, theo quy tắc tổng hợp lực song song cùng chiều, ta có:
P1 + P2 = P = m.g = 60.10 = 600 (N) (2)
Từ (1) và (2) => P1 = 200 N; P2 = 100 N.
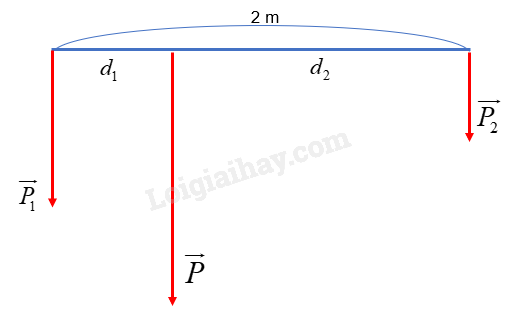
Ta có: d1 + d2 = 2 (3)
Mặt khác, ta có:
\(\frac{{{F_1}}}{{{F_2}}} = \frac{{{d_2}}}{{{d_1}}} \Leftrightarrow \frac{{{d_2}}}{{{d_1}}} = \frac{{{P_1}}}{{{P_2}}}\)
\( \Leftrightarrow \frac{{{d_2}}}{{{d_1}}} = \frac{1}{2} \Rightarrow {d_1} - 2{d_2} = 0\) (4)
Từ (3) và (4) => \(\left\{ \begin{array}{l}{d_1} = \frac{4}{3}\\{d_2} = \frac{2}{3}\end{array} \right.\)
=> Phải treo thùng hàng ở điểm cách vai người đứng sau một khoảng là \(\frac{4}{3}\)m và cách người đứng trước một khoảng \(\frac{2}{3}\)m.

Chọn B.
Gọi F1, F2 là độ lớn của hai lực đặt lên hai đầu của cái gậy. F1, F2 lần lượt cách vai là d1 = 60 cm, d2 = 40 cm.
Ta có: F1 + F2 = mg = 1000 (1)
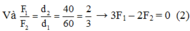
Từ (1) và (2) → F1 = 400 N, F2 = 600 N.

Chọn B.
Gọi F 1 , F 2 là độ lớn của hai lực đặt lên hai đầu của cái gậy. F1, F2 lần lượt cách vai là d 1 = 60 cm, d 2 = 40 cm.
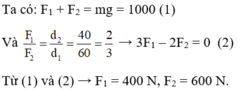

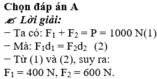



Đáp án C