Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
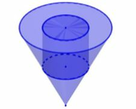
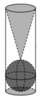
Gọi R,h lần lượt là bán kính đáy và chiều cao của khối trụ ⇒ h = 6 R = 6 . Thể tích của khối trụ là V = πR 2 h = π . 1 2 . 6 = 6 π . Khối cầu bên trong khối trụ có bán kính là R = 1 ⇒ V C = 4 3 π . R 3 = 4 3 π . Khối nón bên trong khối trụ có bán kính đáy là R = 1 và chiều cao h - 2R = 4. Suy ra thể tích khối nón là V N = 1 3 πR 2 h = 1 3 . π . 1 2 . 4 = 4 3 π . Do đó, thể tích lượng nước còn lại bên trong khối trụ là V 0 = V - V C + V N = 6 π - 2 . 4 π 3 = 10 π 3 . Vậy tỉ số cần tính là T = V 0 V = 10 π 3 : 6 π = 5 9 .

Áp dụng định lí Pytago ta tính được
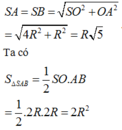
Nửa chu vi tam giác ABC là
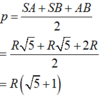
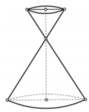
Do khối cầu nằm vừa khít trong hình nón nên bán kính cầu chính bằng bán kính đường tròn nội tiếp tam giác SAB.
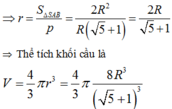
Thể tích khối cầu chính bằng thể tích phần nước dâng lên trong hình trụ có bán kính đáy R.
Gọi h là chiều cao cột nước dâng lên ta có
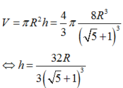
Chọn A.

Đáp án B
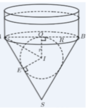
Gọi r , h , r ' , h ' lần lượt là bán kính và chiều cao của hình nón lớn và nhỏ
Phân tích dữ kiện
+) Chiều cao của đồng hồ là 30 cm ⇔ h + h ' = 30 c m
+) Tổng thể tích của đồng hồ là 1000 π c m 3
⇔ V l + V n = π r 2 h + π r ' 2 h ' 3 = 1000 π ⇔ r 2 h + r ' 2 h ' = 3000
+) Đường sinh bất kỳ của hình nón tạo với đáy một góc 60 ° ⇔ h r = h ' r ' = 3
Ta có hệ:
h + h ' = 3 r + r ' r 2 h + r ' 2 h ' = 3 r 3 + r ' 3 = 3000 ⇔ 3 r + r ' 3 = 9000 3 r 3 + r ' 3 = 3000 ⇔ r + r ' 3 r 3 + r ' 3 = 3
⇔ 2 r ' 2 − 5 r r ' + 2 r 2 = 0 ⇔ r r ' = 1 2
vì 0 < r ' < r
Theo đó tỉ lệ cần tính là:
V n V l = r ' 2 h ' r 2 h = r ' r 3 = 1 8

Đáp án D
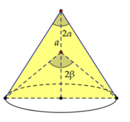
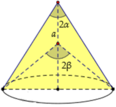
Gọi bán kính đáy là r. Chiều cao của hình nón nhỏ là h 1 = r tan β


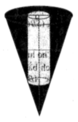
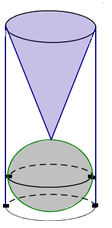
Gọi bán kính đáy của cốc hình trụ là R. Suy ra chiều cao của cốc nước hình trụ là 6R bán kính của viên bi là R; bán kính đáy hình nón là R; chiều cao của hình nón là 4R
Thể tích khối nón là ![]() Thể tích khối nón là
Thể tích khối nón là ![]()
Thể tích của cốc (thể tích lượng nước ban đầu) là ![]()
Suy ra thể tích nước còn lại: ![]() Vậy
Vậy 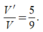
Chọn D.


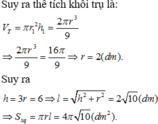

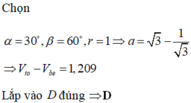
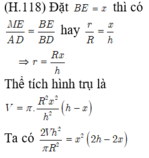

Chọn đáp án A.