Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
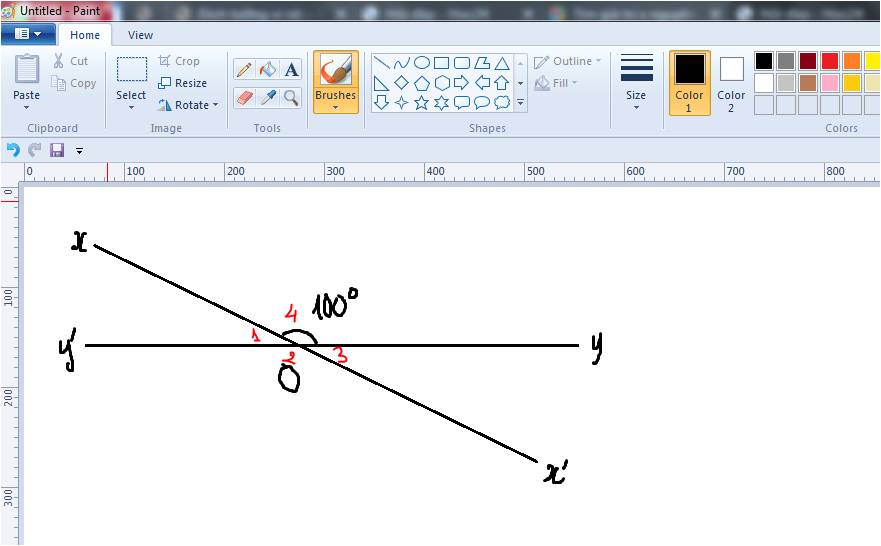
`@)` `\hat{x'Oy'} = \hat{xOy} = 100^@` (hai góc đối đỉnh)
`@)` `\hat{xOy + \hat{xOy'} = 180^@`
hay `100 +` `\hat{xOy'} = 180^@`
`⇒\hat{xOy'} = 180^@ - 100^@ = 80^@`
`@)` `\hat{x'Oy} = \hat{xOy'} = 80^@` (hai góc đối đỉnh)

Vì xOy và xOy' là 2 góc kề bù
=> xOy + xOy' = 180*
Thay xOy = 60*
=> xOy' = 180* - 60*
xOy' = 120*
Vì xx' và yy' cắt nhau tại O
=> xOy và x'Oy' là 2 góc đối đỉnh mà xOy = 60*
=> xOy = x'Oy' = 60*
Vì x'Oy là góc đối đỉnh của xOy' mà xOy' = 120*
=> x'Oy = 120*
Tính rõ rồi nha bạn, nếu cần chứng minh 2 góc đối đỉnh, lm đầy đủ hơn nữa thì bảo mik, cn như này là cx đc điểm tối đa òi
Ta có:
Do \(\widehat{xOy}\) và \(\widehat{xOy'}\) là 2 góc kề bù
\(\Rightarrow\)\(\widehat{xOy}\) + \(\widehat{xOy'}\) = 180o
\(\Rightarrow\)60o + \(\widehat{xOy'}\) = 180o
\(\Rightarrow\)\(\widehat{xOy'}\) = 180o - 60o = 120o
Vậy \(\widehat{xOy'}\)= 120o
Ta có:
Do \(\widehat{xOy}\)và góc \(\widehat{x'Oy'}\) là 2 góc đối đỉnh
\(\Rightarrow\)\(\widehat{xOy}=\widehat{x'Oy'}=60^o\)
Ta có:
Do \(\widehat{xOy}\) và \(\widehat{x'Oy}\) là 2 góc kề bù
\(\Rightarrow\widehat{xOy}+\widehat{x'Oy}=180^o\)
\(\Rightarrow60^o+\widehat{x'Oy}=180^o\)
\(\Rightarrow\widehat{x'Oy}=180^o-60^o=120^o\)
Vậy \(\widehat{x'Oy=120^o}\)
Hoặc bạn có thể giải bằng cách này thì ngắn gọn hơn
Ta có:
Do \(\widehat{xOy'}\) và \(\widehat{x'Oy}\) là hai góc đối đỉnh
\(\Rightarrow\widehat{xOy'}=\widehat{x'Oy}=120^o\)
Vậy \(\widehat{x'Oy}=120^o\)

Giải
_ Ta có \(\widehat{xOy}=\widehat{x'Oy'}=40^0\)( đối đỉnh) => \(\widehat{xOm}=\widehat{mOy}=\widehat{y'On}=\widehat{nOx'}=\frac{40^0}{2}=20^0\)
_ \(\widehat{x'Oy}=\widehat{xOy'}=180^0-40^0=140^0\)

\(\widehat{xOy}+\widehat{x'Oy=180^0}\) (Vì \(\widehat{xOy}\) và \(\widehat{x'Oy}\) là hai góc kề bù)
\(\widehat{xOy}-\widehat{x'Oy}=40^0\)
a.\(\widehat{xOy}=\left(180^0+40^0\right):2=110^0\)
\(\widehat{x'Oy'}=\widehat{xOy}=110^0\) ( 2 góc đối đỉnh)
b. \(\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-110^0=70^0\) (2 góc kề bù)
\(\widehat{xOy'}=\widehat{x'Oy}=70^0\) ( 2 góc đối đỉnh)
ta co
xoy + xoy' = 180
va xoy\xoy' = 5\4
suy ra xoy = 5\4 xoy'
do do 5\4 xoy' + xoy' = 180
xoy' ( 5\4 + 1) = 180
xoy' * 9\4 =180
xoy' = 180 /9/4 = 80 do
vay xoy = 100 do
Thiên Tỷ