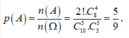Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Tổng số trận đấu trong giải đấu là: ![]()
Sau mỗi trận hòa, tổng số điểm 2 đội nhận được là 1.2 =2.
Sau mỗi trận không hòa, tổng số điểm 2 đội nhận được là 3 + 0 = 3.
Tổng số điểm của tất cả các đội sau khi kết thúc giải đấu là:
65.2 + (182 – 65).3 = 481.

Đáp án C
Do thi đấu vòng tròn 1lượt nên 2 đột bất kỳ chỉ đấu với nhau đúng 1 trận. Số trận đấu của giải là ![]()
Tổng số điểm của 2 đội trong 1 trận hòa là 2 nên tổng số điểm của 23 trận hòa là ![]()
Tổng số điểm của 2 đội trong 1 trận không hòa là 3 nên tổng số điểm của 68 trận không hòa là ![]()
Vậy số điểm trung bình của 1 trận là ![]() (điểm)
(điểm)

Đáp án A
Số vòng đấu là ![]() vòng đấu (gồm cả lượt đi và về)
vòng đấu (gồm cả lượt đi và về)
Mỗi vòng đấu có 7 trận đấu
Do đó có tất cả ![]() trận đấu
trận đấu

Chọn A
+ Chia đều 10 đội vào 2 bảng A và B có ![]() cách.
cách.
Do đó số phần tử của không gian mẫu là : ![]()
+ Sắp xếp đội của lớp 10A1 và 10A2 vào 2 bảng khác nhau A và B có 2! cách.
Chọn 4 đội trong 8 đội còn lại để xếp vào bảng có đội lớp 10A1 có C 8 4 cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau là ![]()
Gọi A là biến cố “Chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau ” thì số các kết quả thuận lợi cho biến cố A là: ![]()
+ Xác suất cần tìm là: