NT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
0
TT
10 tháng 12 2020
Cách 1:Xét tứ giác ADBC có
AB và CD cắt nhau tại O là trung điểm của mỗi đường
=>ADBC là hình bình hành
=>AC//BD(đl)
Cách 2 Chứng minh được \(\Delta AOC=\Delta BOD\left(AO=OC;\widehat{AOC}=\widehat{BOD};OC=OD\right)\)
\(\Rightarrow\widehat{CAO}=\widehat{DBO}\)Hay \(\widehat{CAB}=\widehat{DBA}\)
Hai góc này ở vị trí so le trong bằng nhau
=> AC//BD
CM
14 tháng 2 2019
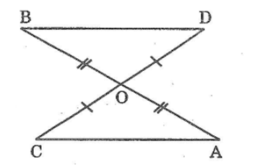
Xét Δ AOC và Δ BOD, ta có:
OA = OB ( Vì O là trung điểm của AB )
∠(AOC) =∠(BOD) (đối đỉnh)
OC = OD ( Vì O là trung điểm của CD)
Suy ra: ΔAOC = ΔBOD (c.g.c)
⇒∠A =∠B (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc so le trong bằng nhau)
22 tháng 11 2016
Ta có hình vẽ:
Xét Δ AOC và Δ BOD có:
OA = OB (gt)
AOC = BOD (đối đỉnh)
OC = OD (gt)
Do đó, Δ AOC = Δ BOD (c.g.c)
=> ACO = ODB (2 góc tương ứng)
Mà ACO và ODB là 2 góc so le trong nên AC // BD (đpcm)
AT
22 tháng 11 2016
Ta có hình vẽ sau:
Xét ΔOAC và ΔOBD có:
OA = OB (gt)
\(\widehat{O_1}\) = \(\widehat{O_2}\) (2 góc đối đỉnh)
OC = OD (gt)
\(\Rightarrow\) ΔOAC = ΔOBD (c.g.c)
\(\Rightarrow\) \(\widehat{C}\) = \(\widehat{D}\) (2 góc tương ứng)
Mà 2 góc này lại ở vị trí so le trong nên
\(\Rightarrow\) AC // BD(đpcm)
SG
2
23 tháng 3 2020
Xét \(\Delta AOD\) và \(\Delta BOC\), ta có: AO = BO (vì O là trung điểm của AB); \(\widehat{AOD}=\widehat{BOC}\) (đối đỉnh); OD = OC (vì O là trung điểm của CD)
\(\Rightarrow\Delta AOD=\Delta BOC\left(c-g-c\right)\)
\(\Rightarrow\widehat{DAO}=\widehat{OBC}\) (2 góc tương ứng)
Mà hai góc này ở vị trí so le cho nên AC // BD.
17 tháng 11 2015
Xét tam giác AOD và BOC có: AO = BO (vì O là trung điểm của AB) ; góc AOD = BOC (đối đỉnh) ; OD = OC (vì O là trung điểm của CD)
=> tam giác AOD = BOC (c - g - c)
=> góc DAO = OBC ( 2 góc tương ứng)
Mà hai góc này ở vị trí so le trong nên AC // BD
4 tháng 7 2021
TRẢ LỜI:
Xét Δ AOC và Δ BOD, ta có:
OA = OB ( Vì O là trung điểm của AB )
∠(AOC) =∠(BOD) (đối đỉnh)
OC = OD ( Vì O là trung điểm của CD)
Suy ra: ΔAOC = ΔBOD (c.g.c)
⇒∠A =∠B (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc so le trong bằng nhau)
4 tháng 7 2021
Xét Δ AOC và Δ BOD có:
OA = OB (gt)
AOC = BOD (đối đỉnh)
OC = OD (gt)
Do đó, Δ AOC = Δ BOD (c.g.c)
=> ACO = ODB (2 góc tương ứng)
Mà ACO và ODB là 2 góc so le trong nên AC // BD (đpcm)
10 tháng 12 2020
Tự vẽ hình.
Do O là trung điểm của AB ➙OA=OB(1)
Do O là trung điểm của DC➙OC=OD(1')
Xét△ACO và △BDO có :
CO=OD(Theo 1')
Góc COA = Góc DOB =90°
AO=OB(Theo 1)
➙△ACO=△BDO (C.G.C)
➙ CA = DB ( hai cạnh tương ứng)(*)
Xét 2 tam giác vuông COB và DOA có
AO=OB (cmt)
CO=OD(cmt)
Góc AOD =góc COB =90°
➙△COB=△DOA ( c.g.c)
➙DA=CB( hai cạnh tương ứng)(**)
Xét △AOC và △BOC có
OC chung
AO=OB (cmt)
➙△AOC=△BOC(c.g.c)
➙AC=CB (***)
Từ (*)(**)(***) suy ra AC=CB=DB=AD (đpcm)
