Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow\dfrac{1}{R_2}=\dfrac{1}{R_{tđ}}-\dfrac{1}{R_1}=\dfrac{1}{3}-\dfrac{1}{6}=\dfrac{1}{6}\)
\(\Rightarrow R_2=6\left(\Omega\right)\)

\(R_1//R_2\)\(\Rightarrow\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow\dfrac{1}{2,4}=\dfrac{1}{6}+\dfrac{1}{R_1}\)
\(\Rightarrow R_1=4\Omega\)
Ta có \(R_{td}=\dfrac{R_1R_2}{R_1+R_2}\) \(\Leftrightarrow2,4=\dfrac{R_16}{R_1+6}\Leftrightarrow2,4\left(R_1+6\right)=6R_1\)
\(\Leftrightarrow2,4R_1+14,4=6R_1\Leftrightarrow-3,6R_1=-14,4\Rightarrow R_1=4\Omega\)

Điện trở tương đương của mạch:
Ta có: \(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Leftrightarrow R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{10.30}{10+30}=7,5\left(\Omega\right)\)

\(\Rightarrow\dfrac{1}{Rtd}=\dfrac{1}{R1}+\dfrac{1}{R2}+....+\dfrac{1}{R2021}\)
\(\Rightarrow\dfrac{1}{Rtd}=\dfrac{1}{1}+\dfrac{1}{\dfrac{1}{2}}+\dfrac{1}{\dfrac{1}{3}}+....+\dfrac{1}{\dfrac{1}{2021}}\)
\(\Rightarrow\dfrac{1}{Rtd}=1+2+3+....+2021\)
\(A=1+2+3+....+2021\)
\(A=2021+2020+2019+...+1\)
\(\Rightarrow2A=2022+2022+...+2022\)(co 2021 so 2022)
\(\Rightarrow2A=2022.2021\Rightarrow A=\dfrac{2022.2021}{2}=2043231\)
\(\Rightarrow\dfrac{1}{Rtd}=A\Rightarrow Rtd=4,89.10^{-7}\left(\Omega\right)\)
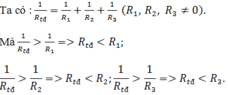

Do mắc song song nên:
\(R_{tđ}=\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}}\)\(\Rightarrow1=\dfrac{1}{\dfrac{1}{3}+\dfrac{1}{R_2}}\)
\(\Rightarrow\dfrac{1}{3}+\dfrac{1}{R_2}=1\Rightarrow\dfrac{1}{R_2}=\dfrac{2}{3}\Rightarrow R_2=1,5\left(\Omega\right)\)