Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Với hai dao động ngược pha, ta luôn có x 1 x 2 = A 1 A 2 → E t 1 E t 2 = A 1 A 2 2 ↔ E 1 − 0 , 56 0 , 08 = 4 → E 1 = 0 , 88 J .

\(W= W_{Cmax}=W_C+W_L\)
=> \(W_L = W_{Cmax}-W_C= \frac{1}{2}C.(U_0^2-u^2)= 5.10^{-7}J.\)

Ta có: \(W=W_t+W_d\)
\(\Leftrightarrow W_t=W_{dmax}-W_d\)
\(=\frac{1}{2}C.U^2_0-\frac{1}{2}Cu^2\)
\(=5.10^{-5}J\)

Độ dời bằng 10% biên độ thì \(|x|=0,1.A\)
A. Do \(a=-\omega^2.x\) nên gia tốc tỉ lệ với li độ, do vậy \(|a|=0,1.A_{max}=10\%.A_{max}\) -->Sai
B. Ta có: \((\dfrac{x}{A})^2+(\dfrac{v}{v_{max}})^2=1\) \(\Rightarrow (0,1)^2+(\dfrac{v}{v_{max}})^2=1\)\(\Rightarrow (\dfrac{v}{v_{max}})^2=0,99\)
\(\Rightarrow \dfrac{v}{v_{max}}=0,995=99,5\%\) -->Đúng.
Vậy chọn B, các ý khác bạn tự thử nhé :)

Hiệu điện thế cực đại giữa hai bản tụ trong khung dao động bằng 6V6V, điện dung của tụ bằng 1μF1μF . Biết dao động điện từ trong khung năng lượng được bảo toàn, năng lượng từ trường cực đại tập trung ở cuộn cảm bằng
A.18.10-6 J.
B.0,9.10-6 J.
C.9.10-6 J.
D.1,8.10-6 J.

Tại thời điểm giữ lò xo thì: \(W_{d}=W_{t}=\dfrac{W}{2}\)
Cố định 1 điểm chính giữa lò xo thì thế năng giảm đi 1 nửa
\(\Rightarrow W_{t'}=\dfrac{W_t}{2}=\dfrac{W}{4};W_{đ}=\dfrac{W}{2}\Rightarrow W'=\dfrac{3W}{4}\)
Có: \(k'=2k\Rightarrow \dfrac{3}{4}.kA^{2}=k'A'^{2}\)
\(\Rightarrow \dfrac{A}{A'}=\dfrac{4}{\sqrt{6}}\)

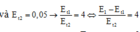
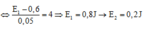
Đáp án A
Với hai dao động ngược pha, ta có: x 1 x 2 = A 1 A 2 = 2 → x 1 x 2 2 = E t 1 E t 2 = 4
Theo giả thuyết bài toán, ta có: E 1 − 0 , 48 0 , 04 = 4 E 1 − 0 , 04 E 2 t = 4 → E 2 t = 0 , 15 J