Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
*Tốc độ cực đại khi đi qua VTCB là:
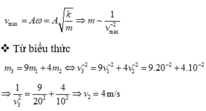
Bình luận: Phương pháp ở trên người ta gọi là phương pháp thuận nghịch.

Đáp án D
Phương pháp: Độ lớn vận tốc cực đại vmax = ωA
Cách giải:
+ Ba lò xo giống hệt nhau, đều có độ cứng là k, khối lượng của các vật tương ứng là m1, m2 và m3
+ Kéo 3 lò xo ra khỏi VTCB một đoạn A rồi thả nhẹ => Biên độ dao động của chúng giống nhau và bằng A
+ Ta có:

+ Theo đề bài ta có:
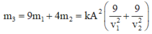
=> Vận tốc của con lắc 3 khi đi qua vị trí cân bằng:



Đáp án C
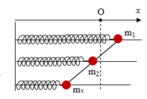
Ta có ω 1 = ω 2 = ω 3 = 10 π rad / s
Phương trình dao động của vật 1 và vật 2 là:
x 1 = 3 cos ( 10 πt - π 2 ) c m x 2 = 1 , 5 cos ( 10 πt ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = ± A )
Trong quá trình dao động cả ba vật nằm trên một đường thẳng khi 2 x 2 = x 1 + x 3 ⇒ x 3 = 2 x 2 - x 1
tính chất trung bình
Bấm máy tính tổng hợp dao động ta được
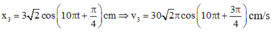
Taị t = 0 và v 30 = - 30 π cm / s
Trường hợp x 2 = 1 , 5 cos ( 10 π t + π ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = - A )
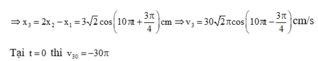

Đáp án B
Độ lớn lực kéo về:
 ;
;
độ lớn lực đàn hồi: F’ = k(∆l + x). Coi chiều dương hướng xuống.
Khi 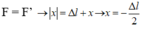 ;
;
Khi lò xo không biến dạng, vận tốc của vật bằng 0
→ x = -A = -∆l
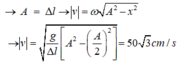

Chọn đáp án B
Áp dụng công thức độc lập với thời gian cho hai thời điểm t 1 v à t 2 ta được:
x 1 2 + v 1 2 ω 2 = x 2 2 + v 2 2 ω 2 ⇔ x 1 2 − x 2 2 = v 2 2 ω 2 − v 1 2 ω 2 ⇒ ω 2 = v 2 2 − v 1 2 x 1 2 − x 2 2 ⇒ ω = v 2 2 − v 1 2 x 1 2 − x 2 2
Do đó, chu kì dao động của vật là T = 2 π ω = 2 π v 2 2 − v 1 2 x 1 2 − x 2 2 = 2 π x 2 2 − x 1 2 v 1 2 − v 2 2

Chọn đáp án B
? Lời giải:
+ Áp dụng công thức độc lập với thời gian cho hai thời điểm t1 và t2 ta được:


Chọn đáp án B
+ Áp dụng công thức độc lập với thời gian cho hai thời điểm t 1 và t 2 ta được:
x 1 2 + v 1 2 ω 2 = x 2 2 + v 2 2 ω 2 ⇔ x 1 2 − x 2 2 = v 2 2 ω 2 − v 1 2 ω 2
⇒ ω 2 = v 2 2 − v 1 2 x 1 2 − x 2 2 ⇒ ω = v 2 2 − v 1 2 x 1 2 − x 2 2
+ Do đó, chu kì dao động của vật là:
T = 2 π ω = 2 π v 2 2 − v 1 2 x 1 2 − x 2 2 = 2 π x 2 2 − x 1 2 v 1 2 − v 2 2
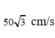
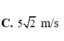
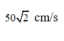
Chọn D
+ Biên độ của cả hai con lắc là A = A1 = A2 vì cùng kéo lệch các vật nặng tới vị trí cách vị trí cân bằng của chúng một đoạn A như nhau và đồng thời thả nhẹ.
+ Khoảng cách đến vị trí cân bằng là |x|, khi khoảng cách từ vật nặng của con lắc đến vị trí cân bằng của chúng đều là b (0 < b < A) thì |x1| = |x2| = b.
+ Từ công thức