Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án B
Phương pháp: Sử dụng công thức tính cơ năng và tần sốgóc của con lắc lò xo
Khoảng cách hai vật trong quá trình dao động ![]()
Cách giải:
Tần số góc của 2 vật: 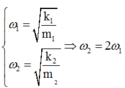
* Biên độ dao động của vật 1 là: 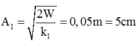
* Biên độ dao động của vật 1 là: 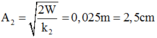
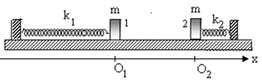
Đặt hệ trục tọa độ chung cho 2 vật như hình vẽ.
Thời điểm ban đầu vật 1 ở biên âm ![]()
Thời điểm ban đầu vật 1 ở biên dương, chú ý tọa độ vị trí cân bằng O2 của vật thứ 2 là L ![]()
Khoảng cách 2 vật trong quá trình dao động là:
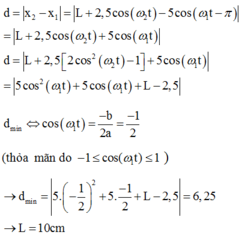

Đáp án A
Biên độ dao động của vật tính từ công thức:
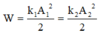
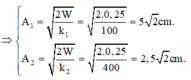
Khoảng cách lúc đầu giữa hai vật là: 10cm.
Chọn gốc thời gian là lúc bắt đầu dao động, chọn gốc tọa độ trùng với O1 thì phương trình dao động của các vật lần lượt là:
![]()
![]()
![]()
Khoảng cách giữa hai vật:
![]()
![]()
Ta thấy y là tam thức bậc hai đối với cos ω t và y m i n = cos ω t = - 0 , 5 Thay vào biểu thức ta tính được
![]()

Hướng dẫn:
Giai đoạn 1: Hai vật dao động điều hòa với biên độ A = 8 cm quanh vị trí cân bằng O từ biên về vị trí cân bằng.
+ Tần số góc dao động của hệ ω = k m 1 + m 2 = k 2 m rad/s.
→ Khi hệ hai vật đến O, ta có v = v m a x = ω A = 8 ω c m / s .
Giai đoạn 1: Vật m1 dao động điều hòa quanh vị trí cân bằng O, vật m2 chuyển động thẳng đều ra xa với tốc độ v 2 = v m a x .
+ Tần số góc của con lắc sau khi vật m 2 tách ra khỏi m 1 ω ' = k m 1 = k m = 2 ω rad/s → T ' = 2 π 2 ω = 2 π ω s.
Tại vị trí vật m 2 tách khỏi vật m 1 , ta có x′ = 0, v ′ = v m a x .
→ Biên độ dao động mới của m 1 là A 1 = v m a x ω ' = 8 ω ω ' = 4 2 cm.
+ Lò xo giãn cực đại lần đầu tiên kể từ thời điểm hai vật tách nhau ứng với Δt = 0,25T s.
→ Khoảng cách giữa hai vật lúc đó là Δ x = x 2 − x 1 = v m a x T ' 4 − A 1 = 8 ω 2 π 4 ω − 4 2 = 3 , 22 cm.
Đáp án D

Đáp án A
Sau khi thả hai vật sẽ cùng chuyển động nhanh dần đến vị trí lò xo không biến dạng (VTCB). Tại VTCB 2 vật sẽ tách nhau ra, vật 1 dao động điều hòa còn vật 2 chuyển động thẳng đều theo chiều cũ với vận tốc bằng vận tốc khi vừa tách nhau.
- Từ lúc thả vật đến lúc lò xo đến VTCB, hệ 2 vật dao động với tần số góc
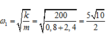 (rad/s).
(rad/s).
- Tại VTCB 2 vật tách ra, khi đó
Vật 2 chuyển động thẳng đều với vận tốc
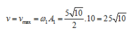 cm/s.
cm/s.
Vật 1 dao động điều hòa với tần số góc mới
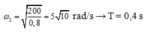
và biên độ mới 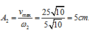
Khi lò xo bị dãn nhiều nhất thì vật 1 đang ở biên → khoảng thời gian chuyển động của vật 2 kể từ lúc 2 vật tách nhau đến lúc lò xo giãn nhiều nhất bằng thời gian vật 1 đi từ VTCB đến biên lần đầu tiên và bằng t = T/4 = 0,4/4 = 0,1 s.
Quãng đường vật 2 đi được trong 0,1 s là
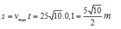
Khoảng cách hai vật khi lò xo giãn cực đại lần đầu là
∆x = 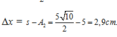

Hướng dẫn:
+ Vật m 2 sẽ rời khỏi m 2 khi hai vật này đi qua vị trí cân bằng tạm lần đầu tiên
→ Tốc độ của vật m 2 tại vị trí này
v 0 = ω X 0 − x 0 = k m 1 + m 2 X 0 − μ m 1 + m 2 g k = 50 0 , 1 + 0 , 4 0 , 1 − 0 , 05 0 , 1 + 0 , 4 .10 50 = 0 , 95
+ Quãng đường m 2 đi được từ khi rời vật m 1 đến khi dừng lại 1 2 m 2 v 0 2 = μ m 2 g S → S = v 0 2 2 μ g = 0 , 9025 m
→ Vậy tổng thời gian từ khi thả vật m 2 đến khi m 2 dừng lại là t = T 4 + 2 S μ g = 2 , 056 s
Đáp án C
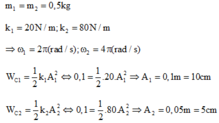
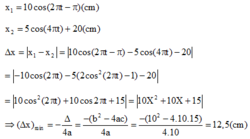




Giải thích: Đáp án B
Phương pháp: Sử dụng lí thuyết về năng lượng dao động của CLLX và dùng tam thức bậc 2 để nhận xét giá trị nhỏ nhất
Cách giải:
Biên độ dao động của các vật tính từ công thức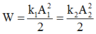
Khoảng cách lúc đầu giữa hai vật: O1O2 = 10 cm.
Chọn gốc thời gian là lúc bắt đầu dao động, chọn gốc tọa độ trùng với O1 thì phương trình dao động của các vật lần lượt là :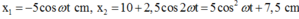 với ω là tần số góc của con lắc thứ nhất.
với ω là tần số góc của con lắc thứ nhất.
Khoảng cách giữa hai vật: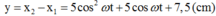
Ta thấy y là tam thức bậc 2 đối với cosωt và ymin khi cosωt = -0,5
Thay cosωt = 0,5 và biểu thức y ta tính được ymin = 6,25 cm.=> Chọn B