Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: Sử dụng định luật bảo toàn cơ năng kết hợp kĩ năng đọc đồ thị
Cách giải: Từ đồ thị ta có:
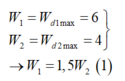
*Hai dao động cùng tần số và vuông pha nhau nên
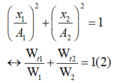
Khi thế năng của hai con lắc bằng nhau ta có:
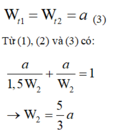
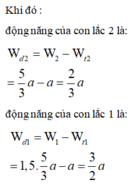
tỉ số động năng con lắc (2) và động năng con lắc (1) là:
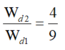
Đáp án C

Đáp án C

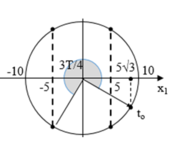
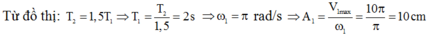

Wđ = 3Wt tại x = ± 5 ứng với 4 điểm trên đường tròn.
Từ t = 0 đến thời điểm thứ 3 động năng = 3 lần thế năng:
+ quay được 3T/4 = 1,5 s
+ đi được quãng đường
![]()


Đáp án A
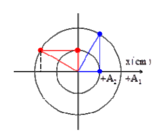
Từ hình vẽ ta thu thập được: F 1 = - 100 x F 2 = - 300 x v à A 1 = 2 A 2 = 1
Khoảng cách giửa hai dao động là lớn nhất khi (l)(2)vuông góc với phương thăng đứng
Tại vị trí này ta thấy rang vật (2) đang có động năng cực đại bang cơ năng, vật 1 đang ở vị trí
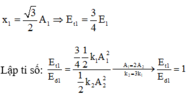

Khoảng thời gian giữa hai lần động năng bằng thế năng là
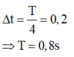
Đáp án D

Giải thích: Đáp án B
Phương pháp:
- Sử dụng lí thuyết về phương trình dao động điều hòa
- Định luật bảo toàn cơ năng
- Công thức tính chu kỉ của con lắc đơn
Cách giải:
Từ đồ thị ta có phương trình dao động của từng vật là: 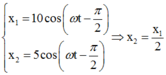
Xét tại thời điểm t ta có: 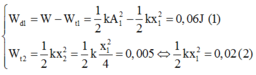
Lấy (2) thế vào (1) ta có: 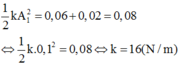
Chu kì của 2 con lắc là: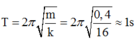
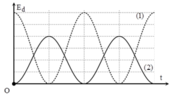
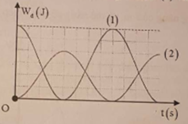

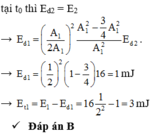
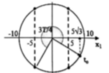
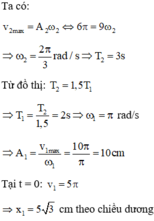


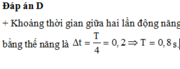
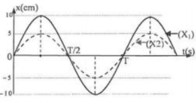
Hướng dẫn:
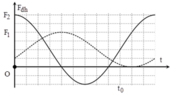
+ Từ đồ thị ta thấy rằng hai dao động này này vuông pha nhau (động năng của vật 1 cực đại – đang ở vị trí cân bằng, thì động năng của vật 2 cực tiểu – đang ở biên) và E 1 = 1 , 5 E 2 .
+ Ta biểu diễn động năng và thế năng của các vật về cơ năng