Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Đáp án C
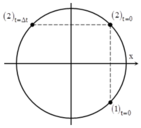
+ Biểu diễn dao động của hai chất điểm tương ứng trên đường tròn
+ Tại t = 0, hai chất điểm ở cùng một vị trí → 1 2 ⊥ Ox (ta không xét đền trường hợp t = 0, hai chất điểm ở cũng một vị trí và chuyển động cùng chiều, vì khi đó hai chất điểm luôn chuyển động cùng nhau ở mọi thời điểm → không có khoảng cách lớn nhất như đề bài đưa ra).
+ Tại thời điểm t = Δt khoảng cách hai chất điểm là lớn nhất → (1)(2) song song với Ox → Δt = 0,25T → Δt = 0,5T.
→ Tốc độ trung bình của chất điểm (2) trong nửa chu kì cũng chính bằng tốc độ trung bình của chất điểm (1) trong một chu kì v tb = 4 cm/s.

Phương trình khoảng cách giữa 2 vật :
\(\Delta x=10\cos\left(\pi t\right)cm\)
Tại thời điểm 2 vật đi ngang qua nhau tức là cùng li độ.
Thời gian ngắn nhất chúng cách nhau thỏa mãn tại thời điểm t1, chúng cùng đi qua VTCB (tốc độ cực đại)
Thời gian \(\Delta x\)từ 0 đến 5cm xác định trên đường tròn
\(t=\frac{T}{12}=\frac{1}{6}s\)
Chọn A

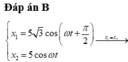
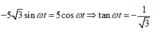
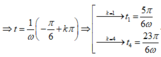
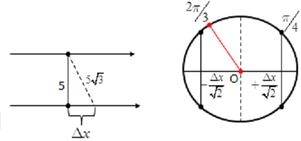
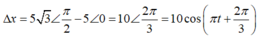
*Ở thời điểm t bất kì nếu hai chất điểm cách nhau 5 3 thì khoảng cách theo phương Ox sẽ là:
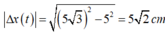
*Một chu kì có 4 lần thõa mãn ∆ x = 5 2 nên lần thứ 2018 sẽ là:
(Số lần / 4 ) = 504 + 2 (1 chu kì có 4 lần ∆ x thỏa mãn ).
*Dựa vào VTLG ta có thời gian lần thứ 2018 thỏa ∆ x = 5 2 cm
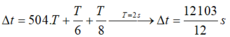

Chọn C


Lúc t = 0 hai chất điểm qua VTCB theo chiều dương (vị trí M 1 , M 2 như hình).
Hai chất điểm gặp nhau ngay sau đó khi chúng ở vị trí M 1 ' , M 2 ' như hình.
![]()

Đáp án C
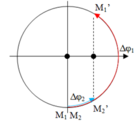

Lúc t = 0 hai chất điểm qua VTCB theo chiều dương (vị trí M1, M2 như hình).
Hai chất điểm gặp nhau ngay sau đó khi chúng ở vị trí ![]() như hình.
như hình.