Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có:

t = 0 lúc 2 chất điểm đồng thời có mặt tại biên dương nên pha ban đầu của 2 chất điểm đều bằng 0.
Phương trình dao động của 2 vật có dạng: x1 = Acos2πt, x2 = Acos2,5πt
Để 2 chất điểm gặp nhau khi chúng đang chuyển động cùng chiều thì:
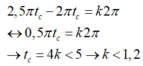
Với k = 1 thì tc = 4s, thay t vào phương trình của x1 và x2 thì ta thấy tại t = 4s hai chất điểm đều ở biên dương, tức chúng đang không chuyển động
→ trong 5 s đầu tiên không có lần nào 2 vật gặp nhau khi đang chuyển động cùng chiều

Chọn C


Lúc t = 0 hai chất điểm qua VTCB theo chiều dương (vị trí M 1 , M 2 như hình).
Hai chất điểm gặp nhau ngay sau đó khi chúng ở vị trí M 1 ' , M 2 ' như hình.
![]()

Đáp án C
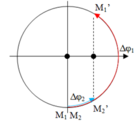

Lúc t = 0 hai chất điểm qua VTCB theo chiều dương (vị trí M1, M2 như hình).
Hai chất điểm gặp nhau ngay sau đó khi chúng ở vị trí ![]() như hình.
như hình.


\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

-TH1: 2 vật cùng ϕ ban đầu. Không mất tính tổng quát giả sử
\(\phi\) = \(\frac{\pi}{3}\)(\(\frac{\pi}{3}\)cũng không ảnh hưởng gì), kết quả như nhau :
+Phương trình dao động vật 1 (có \(f_1=3Hz\) là
\(x_1=Acos\left(2\pi f_1t+\frac{\pi}{3}\right)\)
+Phương trình dao động vật 2 (có f2=6Hz) là
\(f_2=Acos\left(2\pi f_2t+\frac{\pi}{3}\right)\)
=> x1 = x2
\(\Leftrightarrow cos\left(2\pi f_1t+\frac{\pi}{3}\right)=cos\left(2\pi f_2t+\frac{\pi}{3}\right)\)
\(\Leftrightarrow t=\frac{k}{3}=-\frac{1}{27}+\frac{k}{9}\)
\(\Leftrightarrow t_{min1}=\frac{1}{27}s\)
-TH2: 2 vật không cùng ϕ1ban đầu. Không mất tính tổng quát giả sử \(\phi=\frac{\pi}{3}\Rightarrow\phi_2=-\frac{\pi}{3}\)
Giải ra ta được kết quả 1/27 s
\(t=\frac{2\left|\varphi_0\right|}{\omega_1+\omega_2}=\frac{2\frac{\pi}{3}}{6\pi+12\pi}=\frac{1}{27}\)

Đáp án A
Tại 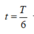 →
→
Chất điểm A có li độ ![]() ;
;
Áp dụng công thức:
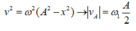
Tại 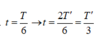 ,
,
với T’ là chu kì của B → B cũng có li độ ![]()
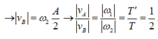


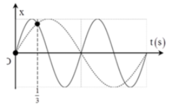


Chọn đáp án A