Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

#) Giải
a/. Ta có: \(vx + vn = \dfrac{S_{AB}}{t_1} = \dfrac{120}{4} = 30 km/h\) ( t1 là thời gian xuôi dòng ) (1)
Và : \(vx - vn = \dfrac{S_{AB}}{t_1+2} = \dfrac{120}{4+2}= 20 km/h\) ( đề nói là quay ngược về thì tăng thêm 2h ) (2)
Từ (1) và (2) suy ra:
( vx - vn ) + ( vx + vn ) = 30 +20
==> 2vx = 50
==> vx = \(\dfrac{50}{2}\) = 25 km/h
P/s: Mk ko chắc.
~ Hok tốt ~
Vận tốc xuôi dòng của ca nô là : 120:4=30 (km/h)
vận tốc ngược dòng của ca nô là : 120:6=20 (km/h)
Gọi vận tốc của ca nô là: x(km/h)
vận tốc dòng nước là :y(km/h)
=> \(x+y=30\)
\(x-y=20\)
\(\Rightarrow x+y+x-y=50\Leftrightarrow2x=50\Leftrightarrow x=25\)
Vậy V của ca nô = 25 km/h

Gọi vận tốc thực của tàu khi nước yên lặng là x km/h (x>o)
vận tốc của thuyền lúc đi là x-4 km/h
vận tốc của thuyền lúc về là x+4 km/h
thời gian thuyền di đến bến bên kia la 80/(x-4) h
thời gian thuyền di được khi quay về la 80/(x+4) h
vì thời gian cả di lẩn về là 8h20' (hay 25/3 h) nên ta có pt:
80/(x+4) + 80/(x-4) = 25/3
<=> 240x-960+240x+960=25x^2-400
<=> 25x^2-480x-400=0
dental' = (-240)^2 +25*400= 67600 (>0) căn dental'= 240
vậy pt có hai nghiệm
x1= (240-260)/25= -0,8 (loại)
x2=(240+260)/25=20 (nhận)
vậy vận tốc của tàu khi nước yên lặng là 20 km/h
Chúc bạn học tốt!!
Gọi Vriêng(canô) là x(km/h).Điều kiện x>4
Vận tốc xuôi: x+ 4
vận tốc ngược x-4
=> Thời gian xuôi: 80/x+4
Thời gian ngược 72/x-4
Ta có pt: 72/(x-4)-80/(x+4)=0,25
<=>72(x+4)-80(x-4)=0,25(x+4)(x-4)
<=>-8x+608=0,25(x²-16)
<=>-32x+2432=x²-16
<=>x²-36x+68x-2448=0
<=>(x-36)(x+68)=0
Giải pt ta được x= 36 ( thỏa mãn)
vậy vận tốc riêng của ca nô là 36 km/h

15 phút = (1/4)giờ
Gọi vận tốc của ca nô khi nước đứng yên là x (km/h). Điều kiện x > 2
Vận tốc ca nô khi xuôi dòng là x + 2 (km/h)
Vận tốc ca nô khi ngược dòng là x – 2 (km/h)
Thời gian ca nô khi xuôi dòng là:
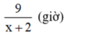
Thời gian ca nô khi ngược dòng là:
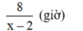
Ta có phương trình:
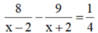
Quy đồng mẫu hai vế:
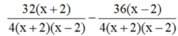
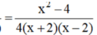
Suy ra:
32x + 64 - 36x + 72 = x2 - 4
⇔ -4x + 136 = x2 - 4
⇔ x2 + 4x - 140 = 0
⇔ (x2 + 4x + 4) - 144 = 0
⇔ (x + 2)2 - 122 = 0
⇔ (x + 14)(x - 10) = 0
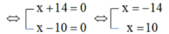
Giá trị x = -14 không thỏa mãn điều kiện
Giá trị x = 10 thỏa mãn điều kiện
Vậy vận tốc của ca nô khi nước yên lặng là 10km/h

Gọi vận tốc thật của cano là x(km/h)
(Điều kiện: x>0)
Vận tốc của cano lúc đi là x+3(km/h)
vận tốc của cano lúc về là x-3(km/h)
Thời gian đi là \(\dfrac{36}{x+3}\left(giờ\right)\)
Thời gian về là \(\dfrac{36}{x-3}\left(giờ\right)\)
Thời gian về nhiều hơn thời gian đi 1 giờ nên ta có phương trình:
\(\dfrac{36}{x-3}-\dfrac{36}{x+3}=1\)
=>\(\dfrac{36x+108-36x+108}{\left(x-3\right)\left(x+3\right)}=1\)
=>\(\left(x-3\right)\left(x+3\right)=216\)
=>\(x^2-9=216\)
=>\(x^2=225\)
=>\(\left[{}\begin{matrix}x=15\left(nhận\right)\\x=-15\left(loại\right)\end{matrix}\right.\)
Vậy: Vận tốc thật của cano là 15km/h

Vận tốc khi đi là x+1,1
Vận tốc lúc về là x-1,1
Tỉ số của thời gian đi và về là:
7/(x+1,1):7/(x-1,1)
=(x-1,1)/(x+1,1)
Dễ lắm bn:
Bài giải:
a) Gọi Vận tốc của ca nô là Vo, vận tốc của dòng nước là Vd
Khi ca nô xuôi dòng
Vo+Vd=120/4=30(km/h)
Khi ca nô ngược dòng
Vo-Vd=120/(4+2)=20(km/h)
Giải hệ pt trên ta được
Vo=25km/h; Vd=5(km/h)
b) Khi ca nô tắt máy đi từ M đến N thì vận tốc lúc này là
Vd=5km/h
Do đó thời gian ca nô tắt máy đi từ M đến N là
T=120/5=24(h).
Đáp số: tự biên tự diễn :D