
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì hai số có tổng bằng 10 và tích bằng -10 nên nó là nghiệm của phương trình: x 2 – 10x – 10 = 0
Ta có: ∆ ' = - 5 2 – 1.(-10) = 25 + 10 = 35 > 0
∆ ' = 35
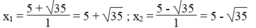
Vậy hai số đó là 5 + 35 và 5 - 35

tìm 2 số có : tổng = 10 và tích = -10
2 số đó là nghiệm của phương trình
x2- 10x - 10 = 0
\(\Delta\) = (-10)2-4.1.(-10) = 100 + 40 = 140 > 0
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
x1= \(\dfrac{10+\sqrt{140}}{2}\) =5 + \(\sqrt{35}\)
x2=\(\dfrac{10-\sqrt{140}}{2}\) =5 - \(\sqrt{35}\)
vậy 2 số đó là :5 + \(\sqrt{35}\) và 5 - \(\sqrt{35}\)


Hai số cần tìm là nghiệm của phương trình x2 - x + 5 = 0
Δ = b2 - 4ac = (-1)2 - 4.1.5 = -19 < 0
⇒ phương trình vô nghiêm
Vậy không tồn tại 2 số có tổng bằng 1 và tích bằng 5

Hai số cần tìm là nghiệm của phương trình x 2 - x + 5 = 0
Δ = b 2 - 4 a c = ( - 1 ) 2 - 4 . 1 . 5 = - 19 < 0
⇒ phương trình vô nghiêm
Vậy không tồn tại 2 số có tổng bằng 1 và tích bằng 5

- Gọi hai số tự nhiên đó là a và b ( \(a,b\in N\) )
Theo bài ra ta có : \(\left\{{}\begin{matrix}a+b=2022\\ab=2021\end{matrix}\right.\)
=> Hệ phương trình có nghiệm là nghiệm của phương trình :
\(X^2-\left(a+b\right)X+ab=X^2-2022X+2021=0\)
\(\Leftrightarrow\left[{}\begin{matrix}X=2021\\X=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=2021\\b=1\end{matrix}\right.\\\left\{{}\begin{matrix}a=1\\b=2021\end{matrix}\right.\end{matrix}\right.\)
Vậy ..
Gọi 1 số là x (x∈N), suy ra số còn lại là 2022-x
Tích 2 số = 2021, nên pt \(x\left(2022-x\right)=2021\)
giải pt :.... tự làm

Ta có:\(\left\{{}\begin{matrix}u+v=15\\u.v=34\end{matrix}\right.\)
u,v là nghiệm của pt: X2 - 15X + 34 = 0
\(\Delta=b^2-4ac=-15^2-4.1.34=-316< 0\)
Vậy pt vô nghiệm

Gọi 2 số đó lần lượt là a ; b
Theo bài ra ta có hệ sau : \(\hept{\begin{cases}a+b=16\\ab=84\end{cases}\Leftrightarrow\hept{\begin{cases}a=16-b\left(1\right)\\ab=84\left(2\right)\end{cases}}}\)
Thế (1) vào (2) ta được :
\(b\left(16-b\right)=84\Leftrightarrow16b-b^2=84\Leftrightarrow b^2-16b+84=0\)
Ta có : \(\Delta=\left(-16\right)^2-4.84=256-336< 0\)
Vậy hệ phương trình vô nghiệm hay ko có 2 số thỏa mãn đề bài
sâu zi, chưa đọc phần comment của bạn bên dưới
Gọi 2 số đó lần lượt là a ; b
Theo bài ra ta có hệ sau : \(\hept{\begin{cases}a+b=16\\ab=64\end{cases}\Leftrightarrow\hept{\begin{cases}a=16-b\left(1\right)\\ab=64\left(2\right)\end{cases}}}\)
Thay (1) vào (2) ta được : \(\left(16-b\right)b=64\Leftrightarrow b^2-16b+64=0\)
Ta có : \(\Delta=\left(-16\right)^2-4.64=256-256=0\)
Vậy phương trình trên có nghiệm kép : \(b=\frac{-\left(-16\right)}{2}=8\)(*)
Thay (*) vào (1) ta được : \(a=16-8=8\)
Vậy hệ phuwong trình có một nghiệm ( a ; b ) = ( 8 ; 8 )
hay 2 số cần tìm là a = 8 ; b = 8

Số đầu tiên là (244+22):2=133
Số thứ hai là 133-22=111
Gọi 2 số đó là a và b
Tổng 2 số là 13 : \(a+b=13\)
Tích 2 số là -90 : \(a.b=-90\)
Suy ra \(\hept{\begin{cases}a+b=13\\ab=-90\end{cases}}\)
\(< =>\hept{\begin{cases}a=13-b\\\left(13-b\right)b=-90\end{cases}}\)
\(< =>\hept{\begin{cases}a=13-b\\b^2-13b-90=0\end{cases}}\)
\(< =>\orbr{\begin{cases}b=18\\b=-5\end{cases}}< =>\hept{\begin{cases}a=-5\\b=18\end{cases}}or\hept{\begin{cases}a=18\\b=-5\end{cases}}\)
Vậy các cặp số ( a,b ) thỏa mãn là ...