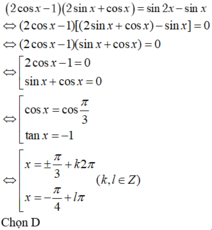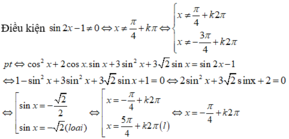K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
24 tháng 7 2021
Lời giải:
PT $\Leftrightarrow (2\cos x-1)(2\sin x+\cos x)=2\sin x\cos x-\sin x$
$\Leftrightarrow (2\cos x-1)(2\sin x+\cos x)=\sin x(2\cos x-1)$
$\Leftrightarrow (2\cos x-1)(\sin x+\cos x)=0$
$\Rightarrow 2\cos x=1$ hoặc $\sin x=-\cos x=\cos (\pi -x)=\sin (x-\frac{\pi}{2})$
Đến đây thì đơn giản rồi.
AH
Akai Haruma
Giáo viên
24 tháng 7 2021
Nkjuiopmli Sv5: Bạn chuyển vế sin x(2cos x-1) sang vế trái thì vế phải còn 0 đó.
PT
1
23 tháng 12 2023
b:
ĐKXĐ: \(\left\{{}\begin{matrix}cosx< >0\\sinx< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< >\dfrac{\Omega}{2}+k\Omega\\x\ne k\Omega\end{matrix}\right.\)
=>\(x\ne\dfrac{\Omega}{2}+\dfrac{k\Omega}{2}\)
\(\dfrac{1}{cosx}+\dfrac{\sqrt{3}}{sinx}=2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot\left[sinx\cdot\cos\dfrac{\Omega}{3}+sin\left(\dfrac{\Omega}{3}\right)\cdot cosx\right]\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot\left(\dfrac{1}{2}\cdot sinx+\dfrac{\sqrt{3}}{2}\cdot cosx\right)\)
=>\(\left(sinx+\sqrt{3}\cdot cosx\right)\left(\dfrac{1}{cosx\cdot sinx}-1\right)=0\)
=>\(2\cdot\left(sinx\cdot\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\cdot cosx\right)\cdot\left(\dfrac{2}{2\cdot sinx\cdot cosx}-1\right)=0\)
=>\(2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\cdot\left(\dfrac{2}{sin2x}-1\right)=0\)
=>\(\left[{}\begin{matrix}sin\left(x+\dfrac{\Omega}{3}\right)=0\\\dfrac{2}{sin2x}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=k\Omega\\sin2x=2\left(loại\right)\end{matrix}\right.\)
=>\(x=-\dfrac{\Omega}{3}+k\Omega\)