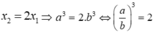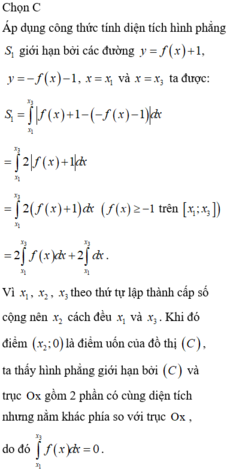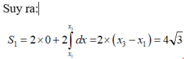Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có thể nghịch suy để chọn hàm làm trắc nghiệm
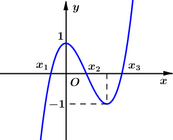
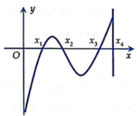
Do \(x_2=\dfrac{x_3-x_1}{2}=1\) nên hàm có dạng: \(y=a\left(x-1\right)^4-b\left(x-1\right)^2+c\) với a;b;c dương
\(y'=0\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=\dfrac{b}{2a}\end{matrix}\right.\) \(\Rightarrow x_1;x_3\) thỏa mãn \(\left(x-1\right)^2=\dfrac{b}{2a}\) và \(f\left(x_2\right)=c\)
\(f\left(x_1\right)+f\left(x_3\right)+\dfrac{2}{3}f\left(x_2\right)=0\Leftrightarrow2f\left(x_1\right)+\dfrac{2}{3}f\left(x_2\right)=0\)
\(\Leftrightarrow a.\left(\dfrac{b}{2a}\right)^2-b\left(\dfrac{b}{2a}\right)+c+\dfrac{c}{3}=0\Rightarrow-\dfrac{b^2}{4a}+\dfrac{4c}{3}=0\)
Tới đây chọn \(a=3;c=1;b=4\) được hàm \(f\left(x\right)=3\left(x-1\right)^4-4\left(x-1\right)^2+1\)
Dễ dàng tính ra \(x_3=1+\sqrt{\dfrac{2}{3}}\) ; \(x_0=1+\sqrt{\dfrac{1}{3}}\) (với \(x_0\) là giao bên phải của đồ thị và trục hoành); \(f\left(x_1\right)=f\left(x_3\right)=-\dfrac{1}{3}\)
\(S_1+S_2=\int\limits^{x_0}_1f\left(x\right)dx-\int\limits^{x_3}_{x_0}f\left(x\right)dx\approx0,41\)
\(\dfrac{S_1+S_2}{S_3+S_4}=\dfrac{0,41}{\left(1+\dfrac{1}{3}\right)\left(x_3-1\right)-0,41}\approx0,6\)

Tiếp tuyến của C vuông góc với đường thẳng y= -x + 2017 nên hệ số góc của tiếp tuyến là k 2 thỏa mãn ( - 1 ) k 2 = - 1 ⇒ k 2 = 1
Suy ra k 2 = y ' = 1 ⇒ 3 x 2 - 4 x + 2 ⇔ 3 x 2 - 4 x + 2 = 0 ( * )
Vì x 1 , x 2 là nghiệm của (*) nên áp dụng Vi-ét ta có x 1 + x 2 = 4 3
Chọn C

Chọn D
![]()
![]()
x 1 , x 2 là hai nghiệm của phương trình y ' = 0
Khi đó, theo định lý Viet, ta có: x 1 + x 2 = 4 .

Chọn D.
Xét phương trình hoành độ hoành độ giao điểm ![]()
Đặt ![]() phương trình (1) trở thành
phương trình (1) trở thành
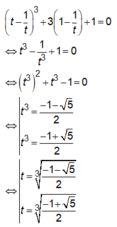
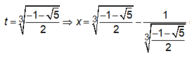
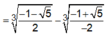
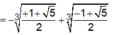
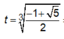
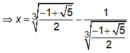
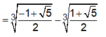
Nên phương trình (1) có một nghiệm.
Vậy số giao điểm của đồ thị hàm số y = x 3 +x+2 và đường thẳng y = -2x + 1 là 1.
Lưu ý: Khi giải trắc nghiệm ta có thể giải phương trình (1) bằng cách bấm máy tinh, ta được 1 nghiệm như sau.
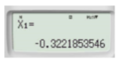
Vậy số giao điểm của đồ thị hàm số y = x 3 +x+2 và đường thẳng y = -2x + 1 là 1.

Chọn D
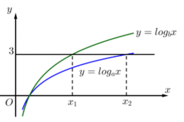
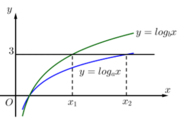
Từ đồ thị có
x
1
là nghiệm của phương trình ![]()
Từ đồ thị có
x
2
là nghiệm của phương trình ![]()
Do