Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
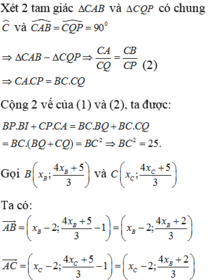
Số các số thuộc tập S là 7.8.8=448. Số rút ra thoả mãn có dạng
A
B
C
¯
với 
Mỗi cách chọn ra bộ ba số thuộc tập {1,...,9} thu được một bộ số (a; b+1; c+2) tương ứng với một bộ ba số (a;b;c) và cho ta một số có ba chữ số thoả mãn yêu cầu bài toán. Vậy có tất cả
C
9
3
số thoả mãn. Xác suất cần tính bằng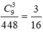 
Chọn đáp án C.
Đáp án C
Từ 8 số đã cho có thể lập được : số có3 chữ số.
Số cần chọn có dạng a b c ¯ trong đó a ≤ b ≤ c .
TH1: a < b < c . Chọn ra 3 số thuộc tập 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ta được 1 số thỏa mãn.
Do đó có C 7 3 = 35 số.
TH2: a = b < c có C 7 2 số thỏa mãn.
TH3: a < b = c có C 7 2 số thỏa mãn.
TH4: a = b = c có C 7 1 số thỏa mãn.
Vậy có: C 7 3 + 2 C 7 2 + C 7 1 = 84 số thỏa mãn chữ số đứng sau luôn lớn hơn bằng chữ số đứng trước.
Vậy xác suất cần tìm là: P = 84 448 = 3 16 .
Xét các số có 9 chữ số khác nhau
Có 9 cách chọn chữ số ở vị trí đầu tiện. Có A 9 8 cách chọn 8 chữ số tiếp theo
Do đó có 9. A 9 8 số có 9 chữ số khác nhau
Gọi A là biến cố: “ số được chọn có đúng bốn chữ số lẻ sao cho số 0 luôn đứng giữa hai chữ số lẻ”
Có C 5 4 cách chọn 4 chữ số lẻ. Đầu tiên la xếp vị trí cho chữ số 0, do chữ số 0 không thể đứng đầu và cuối nên có 7 cách xếp.
Tiếp theo ta có A 4 2 cách chọn và xếp hai chữ số lẻ đứng 2 bên chữ số 0.
Khi đó có 6! Cách xếp 6 chữ số còn lại vào 6 vị trí còn lại.
