Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Phương pháp: Suy ra cách vẽ của đồ thị hàm số y = |f(x – 1) + m| và thử các trường hợp và đếm số cực trị của đồ thị hàm số. Một điểm được gọi là cực trị của hàm số nếu tại đó hàm số liên tục và đổi chiều.
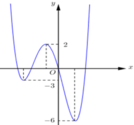
Cách giải: Đồ thị hàm số y = f(x – 1) nhận được bằng cách tịnh tiến đồ thị hàm số y = f(x) sang phải 1 đơn vị nên không làm thay đổi tung độ các điểm cực trị
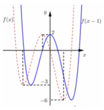
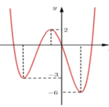
Đồ thị hàm số y = f(x – 1) + m nhận được bằng cách tịnh tiến đồ thị hàm số y = f(x – 1) lên trên m đơn vị nên ta có: yCD = 2 + m; yCT = –3 + m; yCT = –6 + m
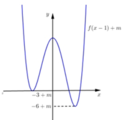
Đồ thị hàm số y = |f(x – 1) + m| nhận được bằng cách từ đồ thị hàm số y = f(x – 1) + m lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành và xóa đi phần đồ thị phía dưới trục hoành.
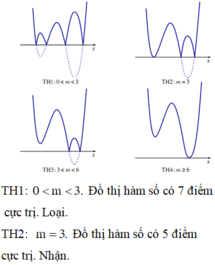
Để đồ thị hàm số có 5 cực trị ![]()
![]()
=>S = {3;4;5} => 3+4+5 = 12

Chọn đáp án A
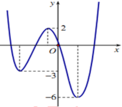
Đồ thị hàm số y=f(x-2019) được tạo thành bằng cách tịnh tiến đồ thị hàm số y=f(x) theo chiều song song với trục Ox sang bên phải 2019 đơn vị.
Đồ thị hàm số y=f(x-2019)+m-2 được tạo thành bằng cách tịnh tiến đồ thị hàm số y=f(x-2019) theo chiều song song với trục Oy lên trên m-2 đơn vị.
Đồ thị hàm số y=|f(x-2019)+m-2| được tạo thành bằng cách giữ nguyên phần đồ thị y=f(x-2019)+m-2 phía trên trục Ox, lấy đối xứng toàn bộ phần đồ thị phía dưới trục Ox qua trục Ox và xóa đi phần đồ thị phía dưới trục Ox.
Do đó để đồ thị hàm số y=|f(x-2019)+m-2| có 5 điểm cực trị thì đồ thị hàm số y=f(x-2019)+m-2 có


Chọn đáp án B.

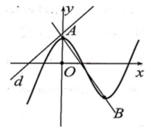
d và (C) cắt nhau tại ba điểm phân biệt

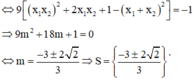
Tổng bình phương các phần tử của S là








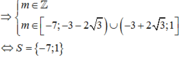



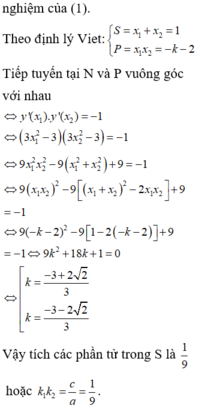
Chọn đáp án B
Phương trình hoành độ giao điểm của đường thẳng d và đồ thị (C):
Đường thẳng d và đồ thị (C) có đúng một điểm chung ⇔ Phương trình (1) có đúng 1 nghiệm khác 1
Vậy tích các phần tử của S bằng 20.