Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Theo đầu bài ta có; b(b2 - a2) = c(c2 - a2)
Hay b3 - c3 = a2(b - c)
Mà b - c ≠ 0 nên b2 + bc + c2 = a2
Theo định lí côsin thì a2 = b2 + c2 - 2bccosA
Do đó: b2 + bc + c2 = b2 + c2 - 2bccosA
Suy ra: cos A = - ½ hay góc A bằng 1200.

1.
Sửa đề: \(S=\dfrac{1}{6}\left(ch_a+bh_c+ah_b\right)\)
\(a.h_a=b.h_b=c.h_c=2S\Rightarrow\left\{{}\begin{matrix}h_a=\dfrac{2S}{a}\\h_b=\dfrac{2S}{b}\\h_c=\dfrac{2S}{c}\end{matrix}\right.\)
\(\Rightarrow6S=\dfrac{2Sc}{a}+\dfrac{2Sb}{c}+\dfrac{2Sa}{b}\)
\(\Leftrightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}=3\)
Mặt khác theo AM-GM: \(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\ge3\sqrt[3]{\dfrac{abc}{abc}}=3\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c\)
\(\Leftrightarrow\) Tam giác đã cho đều
2.
Bạn coi lại đề, biểu thức câu này rất kì quặc (2 vế không đồng bậc)
Ở vế trái là \(2\left(a^2+b^2+c^2\right)\) hay \(2\left(a^3+b^3+c^3\right)\) nhỉ?
3.
Theo câu a, ta có:
\(VT=\dfrac{2S}{a}+\dfrac{2S}{b}+\dfrac{2S}{c}\ge\dfrac{18S}{a+b+c}=\dfrac{18.pr}{a+b+c}=9r\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c\)
Hay tam giác đã cho đều

Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
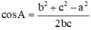
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.

a) Vì a, b, c là độ dài 3 cạnh của một tam giác
⇒ a + c > b và a + b > c (Bất đẳng thức tam giác)
⇒ a + c – b > 0 và a + b – c > 0
Ta có: (b – c)2 < a2
⇔ a2 – (b – c)2 > 0
⇔ (a – (b – c))(a + (b – c)) > 0
⇔ (a – b + c).(a + b – c) > 0 (Luôn đúng vì a + c – b > 0 và a + b – c > 0).
Vậy ta có (b – c)2 < a2 (1) (đpcm)
b) Chứng minh tương tự phần a) ta có :
( a – b)2 < c2 (2)
(c – a)2 < b2 (3)
Cộng ba bất đẳng thức (1), (2), (3) ta có:
(b – c)2 + (c – a)2 + (a – b)2 < a2 + b2 + c2
⇒ b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2 < a2 + b2 + c2
⇒ 2(a2 + b2 + c2) – 2(ab + bc + ca) < a2 + b2 + c2
⇒ a2 + b2 + c2 < 2(ab + bc + ca) (đpcm).

Ta có: \(a\left(a^2-b^2\right)=c\left(b^2-c^2\right)\Leftrightarrow a^3+c^3=b^2c+b^2a\)
\(\Leftrightarrow\left(a+c\right)\left(a^2-ac+c^2\right)=b^2\left(c+a\right)\Leftrightarrow b^2=a^2-ac+c^2\).
Theo định lý hàm cos: \(b^2=a^2+c^2-2cos\widehat{B}.ac\).
Do đó \(cos\widehat{B}=\dfrac{1}{2}\) hay \(\widehat{B}=60^o\).

Xét tam thức f(x) = b2x2 - (b2 + c2 - a2)x + c2 có:
Δ = (b2 + c2 - a2)2 - 4b2c2
= (b2 + c2 - a2 - 2bc)(b2 + c2 - a2 + 2bc)
= [(b - c)2 - a2][(b + c)2 - a2]
= (b – c – a)(b – c + a)(b + c + a)(b + c – a).
Do a, b, c là 3 cạnh của tam giác nên theo bất đẳng thức tam giác ta có:
b < c + a ⇒ b – c – a < 0
c < a + b ⇒ b – c + a > 0
a < b + c ⇒ b + c – a > 0
a, b, c > 0 ⇒ a + b + c > 0
⇒ Δ < 0 ⇒ f(x) cùng dấu với b2 ∀x hay f(x) > 0 ∀x (đpcm).

Chọn B.
Ta có:
a(a2 – c2) = b(b2 – c2) ⇔ a3 – ac2 = b3 – bc2
⇔ a3 – b3 = ac2 – bc2
⇔ (a – b)(a2 + ab + b2) = c2(a – b)
⇔ a2 + ab + b2 = c2
⇔ ab = c2 – a2 – b2
Ta lại có: 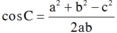
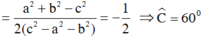
Chọn A.
Áp dụng công thức độ dài đuờng trung tuyến ta có