Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho 3 điểm A, B, C. Gọi O là trung điểm của đoạn thẳng AB. Chứng minh rằng nếu 4MO2=AB2 thì MA ⊥ MB.

\(4MO^2=AB^2\Leftrightarrow\left(2\overrightarrow{MO}\right)^2=\left(\overrightarrow{AM}+\overrightarrow{MB}\right)^2\)
\(\Leftrightarrow\left(\overrightarrow{MA}+\overrightarrow{MB}\right)^2=\left(\overrightarrow{AM}+\overrightarrow{MB}\right)^2\)
\(\Leftrightarrow MA^2+MB^2+2\overrightarrow{MA}.\overrightarrow{MB}=AM^2+BM^2+2\overrightarrow{AM}.\overrightarrow{MB}\)
\(\Leftrightarrow4\overrightarrow{MA}.\overrightarrow{MB}=0\Leftrightarrow\overrightarrow{MA}.\overrightarrow{MB}=0\)
\(\Leftrightarrow MA\perp MB\)

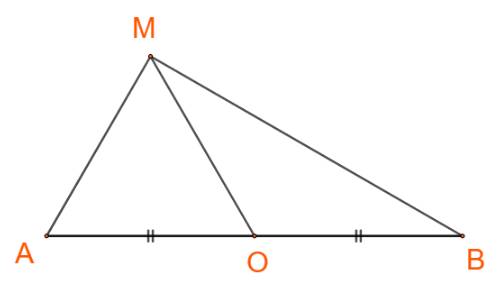
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \Leftrightarrow - \overrightarrow {OA} = \overrightarrow {OB} \)
\(\Rightarrow {\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right)\left( {\overrightarrow {MO} - \overrightarrow {OA} } \right) \\= \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) = \overrightarrow {MA} .\overrightarrow {MB} \) (đpcm)


\(\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EA} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EB} } \right)\\ + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FC} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FD} } \right)\end{array}\)
\( = \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} \overrightarrow { + MG} } \right) + 2\left( {\overrightarrow {GE} + \overrightarrow {GF} } \right) \\+ \left( {\overrightarrow {EA} + \overrightarrow {EB} } \right) + \left( {\overrightarrow {FC} + \overrightarrow {FD} } \right)\)
\( = 4\overrightarrow {MG} + 2.\overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MG} \) (đpcm)

Ta có:
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{MB}+4\overrightarrow{MC}\)
\(=6\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{IB}+4\overrightarrow{IC}\)
\(=6\overrightarrow{MI}+4\overrightarrow{IG}+4\overrightarrow{IC}\)
\(=6\overrightarrow{MI}\)
\(\Rightarrow M,I,N\) thẳng hàng

Tham khảo:
a) Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} + \left( {\overrightarrow {MA} + \overrightarrow {AB} } \right) + 2\left( {\overrightarrow {MA} + \overrightarrow {AC} } \right) = \overrightarrow 0 \)
\(\begin{array}{l} \Leftrightarrow 4\overrightarrow {MA} + \overrightarrow {AB} + 2\overrightarrow {AC} = \overrightarrow 0 \\ \Leftrightarrow 4\overrightarrow {AM} = \overrightarrow {AB} + 2\overrightarrow {AC} \\ \Leftrightarrow \overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \end{array}\)
Trên cạnh AB, AC lấy điểm D, E sao cho \(AD = \frac{1}{4}AB;\;\,AE = \frac{1}{2}AC\)
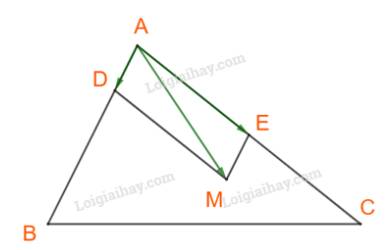
Khi đó \(\overrightarrow {AM} = \overrightarrow {AD} + \overrightarrow {AE} \) hay M là đỉnh thứ tư của hình bình hành AEMD.
b) Chứng minh rằng với mọi điểm O, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM} \)
Với mọi điểm O, ta có: \(\left\{ \begin{array}{l}\overrightarrow {OA} = \overrightarrow {OM} + \overrightarrow {MA} ;\;\\\overrightarrow {OB} = \overrightarrow {OM} + \overrightarrow {MB} ;\;\,\\\overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {MC} \end{array} \right.\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = \left( {\overrightarrow {OM} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + 2\left( {\overrightarrow {OM} + \overrightarrow {MC} } \right)\\ = 4\overrightarrow {OM} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} } \right) = 4\overrightarrow {OM} + \overrightarrow 0 = 4\overrightarrow {OM} .\end{array}\)
Vậy với mọi điểm O, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM} \).
Tham khảo cách 2 câu a:
Cách 2:
Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \left( {\overrightarrow {MC} + \overrightarrow {CA} } \right) + \left( {\overrightarrow {MC} + \overrightarrow {CB} } \right) + 2\overrightarrow {MC} = \overrightarrow 0 \)
\(\begin{array}{l} \Leftrightarrow 4\overrightarrow {MC} + \overrightarrow {CA} + \overrightarrow {CB} = \overrightarrow 0 \\ \Leftrightarrow 4.\overrightarrow {CM} = \overrightarrow {CA} + \overrightarrow {CB} \end{array}\)
Gọi D là đỉnh thứ tư của hình bình hành ACBD.
Khi đó: \(\overrightarrow {CD} = \overrightarrow {CA} + \overrightarrow {CB} \)\( \Rightarrow 4.\overrightarrow {CM} = \overrightarrow {CD} \)
\( \Leftrightarrow \overrightarrow {CM} = \frac{1}{4}\overrightarrow {CD} \Leftrightarrow \overrightarrow {CM} = \frac{1}{2}\overrightarrow {CO} \)
Với O là tâm hình bình hành ACBD, cũng là trung điểm đoạn AB.
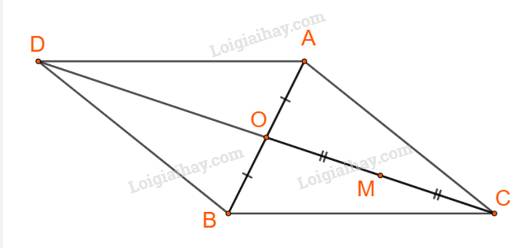
Vậy M là trung điểm của trung tuyến kẻ từ C của tam giác ABC.