K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
0
21 tháng 1 2022
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
SUy ra: AB//CD
27 tháng 6 2023
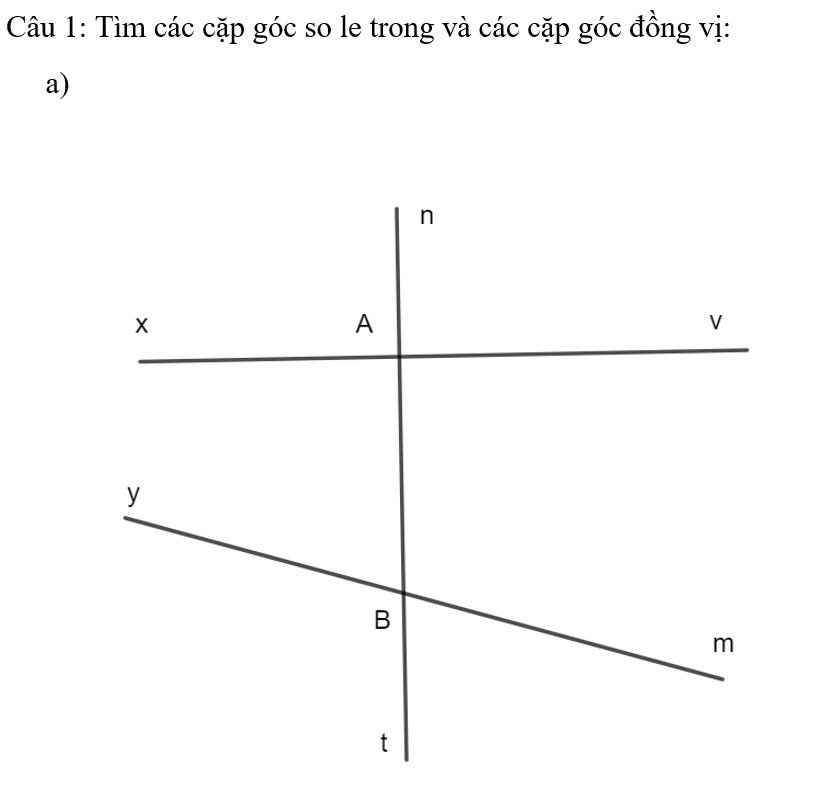
a: So le trong: góc vAB và góc yBA; góc xAB và góc mBA
ĐỒng vị: góc nAx và góc yBA; góc nAv và góc mBA; góc xAB và góc tBy; góc vAB và góc mBt
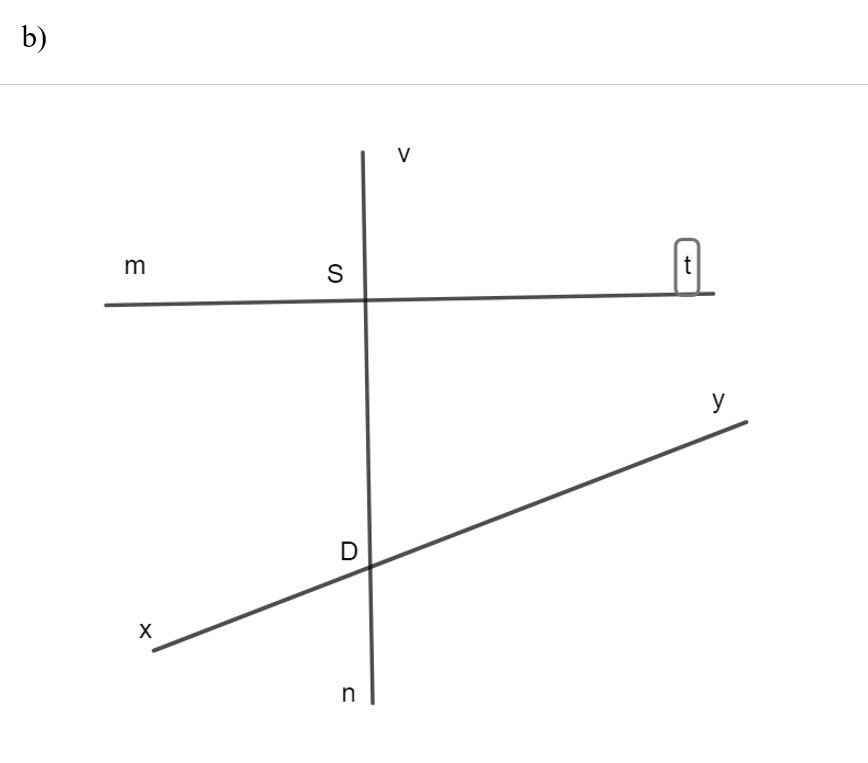
b: So le trong: góc mSD và góc yDS; góc tSD và góc xDS
ĐỒng vị: góc vSm và góc xDv; góc vSt và góc vDy; góc mSn và góc xDn; góc tSD và góc yDn
DR
27 tháng 6 2023
a)Cặp so le trong: xAB và ABm, vAB và ABy
Cặp đồng vị: nAx và ABy, nAv và ABm, xAB và yBt,vAB và mBt
b)Cặp so le trong: mSD và SDy, tSD và SDx
Cặp đồng vị: vSm và SDx, vSt và SDy, nDx và DSm,nDy và DSt
17 tháng 1 2022
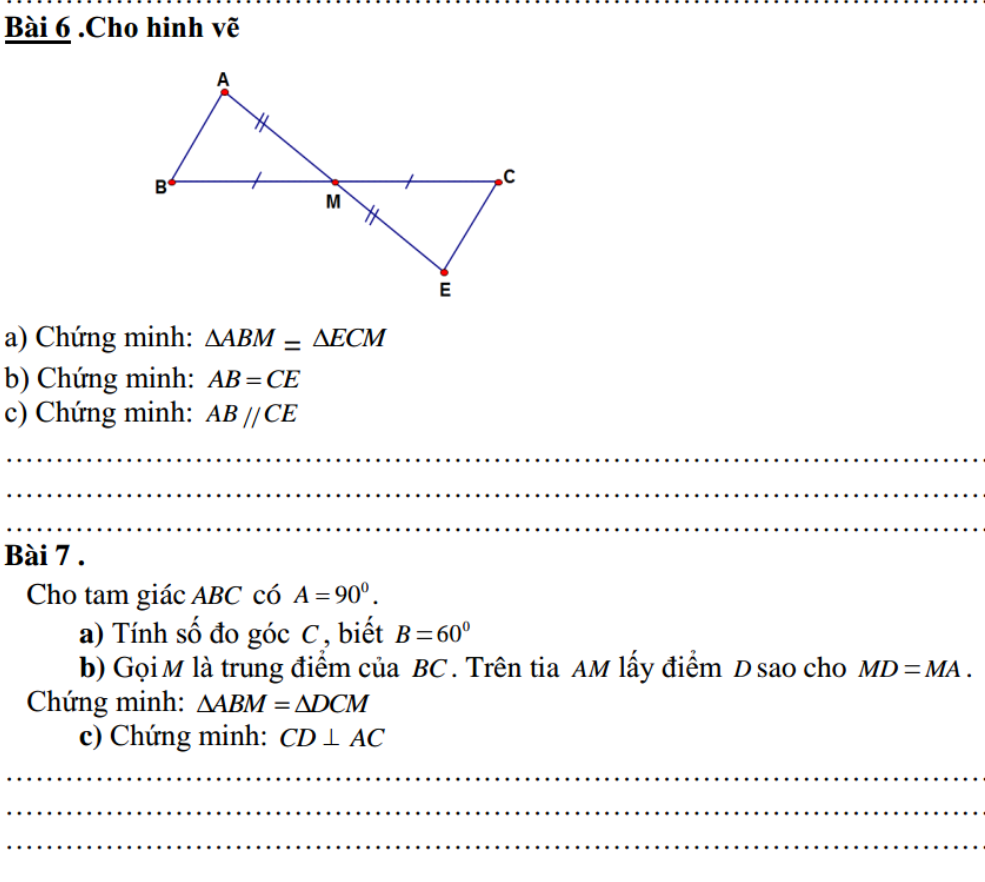
a, Xét tam giác ABM và tam giác ECM
^AMB = ^EMC ( đối đỉnh )
BM = MC ( gt )
AM = ME ( gt )
Vậy tam giác ABM = tam giác ECM ( c.g.c )
b, Vì tam giác ABM = tam giác ECM ( cma )
=> AB = EC
c, Vì tam giác ABM = tam giác ECM ( cma )
=> ^ABM = ^ECM
mà 2 góc này ở vị trí so le trong => AB // CE
8 tháng 7 2023
a: BC=căn 6^2+8^2=10cm
b: Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
c: ΔMAB=ΔMDC
=>góc MAB=góc MDC
=>AB//CD
=>DC vuông góc AC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được;
\(\dfrac{a}{14}=\dfrac{b}{12}=\dfrac{c}{13}=\dfrac{d}{15}=\dfrac{d-b}{15-13}=\dfrac{6}{2}=3\)
Do đó: a=42; b=36; c=39; d=45