K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BA
1
20 tháng 7 2023
Ta có:
\(\dfrac{1}{cos^2x-sin^2x}+\dfrac{2tanx}{1-tan^2x}=\dfrac{1}{cos2x}+tan2x=\dfrac{1}{cos2x}+\dfrac{sin2x}{cos2x}=\dfrac{1+sin2x}{cos2x}=\dfrac{cos2x}{1-sin2x}\)
\(\Rightarrow P=a+b=2+1=3\)
BA
1
21 tháng 7 2023
4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7
31 tháng 8 2021
cos2x - (2m + 1)cosx + m + 1 = 0
⇔ 2cos2x - (2m + 1).cosx = 0
⇔ \(\left[{}\begin{matrix}cosx=0\left(1\right)\\2cosx=2m+1\left(2\right)\end{matrix}\right.\)
(1) ⇔ \(x=\dfrac{\pi}{2}+k\pi\) với k thuộc Z. Mà \(x\in\left(\dfrac{\pi}{2};2\pi\right)\)
⇒ x = \(\dfrac{3\pi}{2}\)
Như vậy đã có 1 nghiệm trên \(\left(\dfrac{\pi}{2};2\pi\right)\) đó là x = \(\dfrac{3\pi}{2}\). Bây giờ cần tìm m để (2) có 2 nghiệm phân biệt trên \(\left(\dfrac{\pi}{2};2\pi\right)\) và trong 2 nghiệm đó không có nghiệm x = \(\dfrac{3\pi}{2}\). Tức là x = \(\dfrac{3\pi}{2}\) không thỏa mãn (2), tức là
2m + 1 ≠ 0 ⇔ \(m\ne-\dfrac{1}{2}\)
(2) ⇔ \(2.\left(2cos^2\dfrac{x}{2}-1\right)=2m+1\)
⇔ \(4cos^2\dfrac{x}{2}=2m+3\)
Do x \(\in\left(\dfrac{\pi}{2};2\pi\right)\) nên \(\dfrac{x}{2}\in\left(\dfrac{\pi}{4};\pi\right)\) nên cos\(\dfrac{x}{2}\) ∈ \(\left(-1;\dfrac{\sqrt{2}}{2}\right)\)
Đặt cos\(\dfrac{x}{2}\) = t ⇒ t ∈ \(\left(-1;\dfrac{\sqrt{2}}{2}\right)\). Ta được phương trình : 4t2 = 2m + 3
Cần tìm m để [phương trình được bôi đen] có 2 nghiệm t ∈ \(\left(-1;\dfrac{\sqrt{2}}{2}\right)\)
Dùng hàm số bậc 2 là ra. Nhớ kết hợp điều kiện \(m\ne-\dfrac{1}{2}\)
MT
2
26 tháng 8 2021
Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF
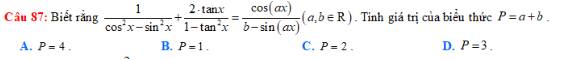
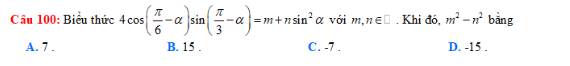
ta có :