
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




21.
\(\left\{{}\begin{matrix}SA\perp AB\\AC\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAC\right)\)
E là trung điểm SA, F là trung điểm SB \(\Rightarrow\) EF là đường trung bình tam giác SAB
\(\Rightarrow EF||AB\Rightarrow EF\perp\left(SAC\right)\)
\(\Rightarrow EF=d\left(F;\left(SEK\right)\right)\)
\(SE=\dfrac{1}{2}SA=\dfrac{3a}{2}\) ; \(EF=\dfrac{1}{2}AB=a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{13}\Rightarrow SK=\dfrac{2}{3}SC=\dfrac{2a\sqrt{13}}{3}\)
\(\Rightarrow S_{SEK}=\dfrac{1}{2}SE.SK.sin\widehat{ASC}=\dfrac{1}{2}.\dfrac{3a}{2}.\dfrac{2a\sqrt{13}}{3}.\dfrac{2a}{a\sqrt{13}}=a^2\)
\(\Rightarrow V_{S.EFK}=\dfrac{1}{3}EF.S_{SEK}=\dfrac{1}{3}.a.a^2=\dfrac{a^3}{3}\)
\(AB\perp\left(SAC\right)\Rightarrow AB\perp\left(SEK\right)\Rightarrow AB=d\left(B;\left(SEK\right)\right)\)
\(\Rightarrow V_{S.EBK}=\dfrac{1}{3}AB.S_{SEK}=\dfrac{1}{3}.2a.a^2=\dfrac{2a^3}{3}\)
22.
Gọi D là trung điểm AB
Do tam giác ABC đều \(\Rightarrow CD\perp AB\Rightarrow CD\perp\left(SAB\right)\)
\(\Rightarrow CD=d\left(C;\left(SAB\right)\right)\)
\(CD=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
N là trung điểm SC \(\Rightarrow d\left(N;\left(SAB\right)\right)=\dfrac{1}{2}d\left(C;\left(SAB\right)\right)=\dfrac{a\sqrt{3}}{2}\)
\(S_{SAB}=\dfrac{1}{2}SA.AB=a^2\sqrt{3}\) \(\Rightarrow S_{SAM}=\dfrac{1}{2}S_{SAB}=\dfrac{a^2\sqrt{3}}{2}\)
\(\Rightarrow V_{SAMN}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.\dfrac{a^2\sqrt{3}}{2}=\dfrac{a^3}{4}\)
Lại có:
\(V_{SABC}=\dfrac{1}{3}SA.S_{ABC}=\dfrac{1}{3}.a\sqrt{3}.\dfrac{\left(2a\right)^2\sqrt{3}}{4}=a^3\)
\(\Rightarrow V_{A.BCMN}=V_{SABC}-V_{SANM}=\dfrac{3a^3}{4}\)


c: Xét ΔAKB vuông tại K có KM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AK^2\left(1\right)\)
Xét ΔAKC vuông tại K có KN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AK^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
hay \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN và ΔACB có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN\(\sim\)ΔACB


Chọn \(\overrightarrow{u_d}=\left(2;5;1\right)\) ; \(\overrightarrow{u_{d'}}=\left(-1;3;-1\right)\)
Gọi \(A\left(3;3;1\right)\) là 1 điểm thuộc d và \(B\left(2;-3;-1\right)\) là 1 điểm thuộc d'
\(\Rightarrow\overrightarrow{BA}=\left(1;6;2\right)\)
(Để chứng minh d và d' chéo nhau thì ta chỉ cần kiểm tra tích hỗn hợp \(\left[\overrightarrow{u_d};\overrightarrow{u_{d'}}\right].\overrightarrow{BA}\ne0\))
Ta có: \(\left[\overrightarrow{u_d};\overrightarrow{u_{d'}}\right]=\left(-8;1;11\right)\)
\(\Rightarrow\left[\overrightarrow{u_d};\overrightarrow{u_{d'}}\right].\overrightarrow{BA}=-8.1+6.1+2.11=20\ne0\)
\(\Rightarrow\) d và d' là 2 đường thẳng chéo nhau

\(5\left(x^2+y^2+z^2\right)=9\left(xy+2yz+zx\right)\\ \Leftrightarrow5x^2+5\left(y^2+z^2\right)-9x\left(y+z\right)-18yz=0\\ \Leftrightarrow5x^2-9x\left(y+z\right)=18yz-5\left(y^2+z^2\right)\)
Ta có \(yz\le\dfrac{\left(y+z\right)^2}{4};y^2+z^2\ge\dfrac{\left(y+z\right)^2}{2}\)
\(\Leftrightarrow18yz-5\left(y^2+z^2\right)\le\dfrac{9\left(y+z\right)^2}{2}-\dfrac{5\left(y+z\right)^2}{2}=2\left(y+z\right)^2\\ \Leftrightarrow5x^2-9x\left(y+z\right)\le2\left(y+z\right)^2\\ \Leftrightarrow5x^2-9x\left(y+z\right)-2\left(y+z\right)^2\le0\\ \Leftrightarrow\left[x-2\left(y+z\right)\right]\left(5x+y+z\right)\le0\\ \Leftrightarrow x-2\left(y+z\right)\le0\left(x,y,z>0\right)\\ \Leftrightarrow x\le2\left(y+z\right)\)
Ta có \(P=\dfrac{x}{y^2+z^2}-\dfrac{1}{\left(x+y+z\right)^3}\le\dfrac{x}{\dfrac{\left(y+z\right)^2}{2}}-\dfrac{1}{\left(x+y+z\right)^3}\)
\(\Leftrightarrow P\le\dfrac{2x}{\left(y+z\right)^2}-\dfrac{1}{\left[2\left(y+z\right)+y+z\right]^3}\le\dfrac{4\left(y+z\right)}{\left(y+z\right)^2}-\dfrac{1}{27\left(y+z\right)^3}\\ \Leftrightarrow P\le\dfrac{4}{y+z}-\dfrac{1}{27\left(y+z\right)^3}\)
Đặt \(t=\dfrac{1}{y+z}>0\Leftrightarrow P\le4t-\dfrac{t^3}{27}\)
\(\Leftrightarrow16-P\ge16-4t+\dfrac{t^3}{27}=\dfrac{t^3-108t+432}{27}\\ \Leftrightarrow16-P\ge\dfrac{\left(t+12\right)\left(t-6\right)^2}{27}\ge0\left(t>0\right)\\ \Leftrightarrow P\le16\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{3};y=z=\dfrac{1}{12}\)


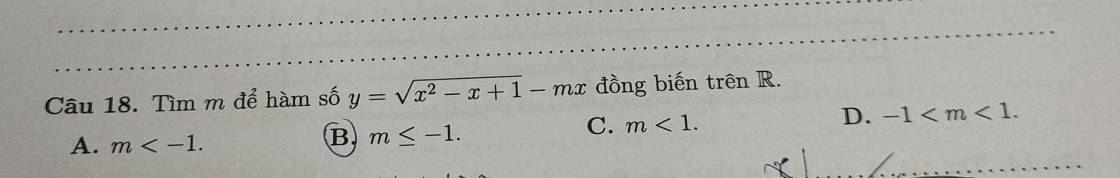


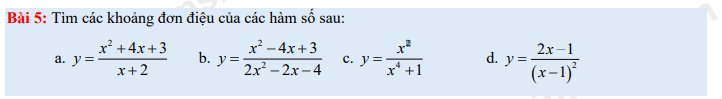
 Giúp với
Giúp với
 giúp mk với :(((((((((((
giúp mk với :(((((((((((
70.
\(2^x>3^x\Leftrightarrow x.ln2>x.ln3\)
\(\Leftrightarrow x\left(ln3-ln2\right)< 0\)
\(\Leftrightarrow x< 0\)
71.
ĐKXĐ: \(\left\{{}\begin{matrix}3x-2>0\\6-5x>0\end{matrix}\right.\) \(\Rightarrow\dfrac{2}{3}< x< \dfrac{6}{5}\)
\(log_2\left(3x-2\right)>log_2\left(6-5x\right)\)
\(\Leftrightarrow3x-2>6-5x\)
\(\Leftrightarrow8x>8\)
\(\Leftrightarrow x>1\)
Kết hợp ĐKXĐ ta được: \(1< x< \dfrac{6}{5}\)
72.
ĐKXĐ: \(x>0\)
\(log_2x+log_4x=3\)
\(\Leftrightarrow log_2x+\dfrac{1}{2}log_2x=3\)
\(\Leftrightarrow\dfrac{3}{2}log_2x=3\)
\(\Leftrightarrow log_2x=2\)
\(\Leftrightarrow x=4\)
73.
\(2^x+2^{x-1}+2^{x-2}=3^x-3^{x-1}+3^{x-2}\)
\(\Leftrightarrow2^x+\dfrac{1}{2}.2^x+\dfrac{1}{4}.2^x=3^x-\dfrac{1}{3}.3^x+\dfrac{1}{9}.3^x\)
\(\Leftrightarrow\dfrac{7}{4}.2^x=\dfrac{7}{9}.3^x\)
\(\Leftrightarrow2^{x-2}=3^{x-2}\)
\(\Leftrightarrow\left(x-2\right).ln2=\left(x-2\right).ln3\)
\(\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\)