K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QN
1
13 tháng 1 2022
\(=\dfrac{x^2-4y}{xy}\cdot\dfrac{x^2}{x-y}=\dfrac{x\left(x^2-4y\right)}{y\left(x-y\right)}\)
T
5 tháng 9 2023
4. \(x^2-3x+xy-3y=0\)
\(\Leftrightarrow x\left(x-3\right)+y\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+y=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-y\end{matrix}\right.\)
5. \(x^2-8x-3x+24=0\)
\(\Leftrightarrow x\left(x-8\right)-3\left(x-8\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-8=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\)
6. \(\left(x-2\right)^2-5\left(2-x\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2+5\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-2+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-2+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
7. \(3x\left(x-1\right)-x^2+2x-1=0\)
\(\Leftrightarrow3x\left(x-1\right)-\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow3x\left(x-1\right)-\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left[3x-\left(x-1\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{2}\end{matrix}\right.\)
8. \(x^2\left(x-3\right)+18-6x=0\)
\(\Leftrightarrow x^2\left(x-3\right)-6\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x^2-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\pm\sqrt{6}\end{matrix}\right.\)
10. \(\left(x-5\right)^2-\left(x-2\right)^2=0\)
\(\Leftrightarrow\left[\left(x-5\right)-\left(x-2\right)\right]\left[\left(x-5\right)+\left(x-2\right)\right]=0\)
\(\Leftrightarrow\left(x-5-x+2\right)\left(x-5+x-2\right)=0\)
\(\Leftrightarrow-3\left(2x-7\right)=0\)
\(\Leftrightarrow2x-7=0\)
\(\Leftrightarrow x=\dfrac{7}{2}\)
12. \(x^2\left(x-3\right)-4x+12=0\)
\(\Leftrightarrow x^2\left(x-3\right)-4\left(x-3\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=3\end{matrix}\right.\)
14. \(3x^2-7x-10=0\)
\(\Leftrightarrow3x^2+3x-10x-10=0\)
\(\Leftrightarrow3x\left(x+1\right)-10\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\3x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{10}{3}\end{matrix}\right.\)
#Urushi
5 tháng 9 2023
4: x^2-3x+xy-3y=0
=>x(x-3)+y(x-3)=0
=>(x-3)(x+y)=0
=>x=3 và x+y=0
=>x=3 và y=-3
6: (x-2)^2-5(2-x)=0
=>(x-2)^2+5(x-2)=0
=>(x-2)(x-2+5)=0
=>(x-2)(x+3)=0
=>x=-3 hoặc x=2
8: x^2(x-3)+18-6x=0
=>x^2(x-3)-6(x-3)=0
=>(x-3)(x^2-6)=0
=>x=3 hoặc \(x=\pm\sqrt{6}\)
10: (x-5)^2-(x-2)^2=0
=>(x-5-x+2)(x-5+x-2)=0
=>-3(2x-7)=0
=>2x-7=0
=>x=7/2
12: x^2(x-3)-4x+12=0
=>x^2(x-3)-4(x-3)=0
=>(x-3)(x^2-4)=0
=>(x-3)(x-2)(x+2)=0
=>\(x\in\left\{3;2;-2\right\}\)
14: 3x^2-7x-10=0
=>3x^2-10x+3x-10=0
=>(3x-10)(x+1)=0
=>x=10/3 hoặc x=-1
NY
1
17 tháng 3 2022
a, Gọi chiều rộng ban đầu là x(m) x>0
Chiều dài ban đầu : x+10(m)
Chiều rộng sau khi được tăng: x+5(m)
Chiều dài sau khi giảm: x+10-2=x+8(m)
Theo bài ra ta có pt
(x+8)(x+5)-x(x+10)=100
Giải ra được x=20(m)
Chiều dài : 20=10=30(m)
Diện tích mảnh vườn:20.30=600(m\(^2\))
b, Gọi vận tốc trung bình của xe mày là x(km/h) x>0
Vận tốc tb của ô tô là : x+6(km/h)
Theo bài ra ta có pt
2x+2(x+6)=140
Giải ra được x=32(km/h)
Vtb của ô tô là 32+6=38(km/h)
H
2
18 tháng 10 2023
Xét tứ giác ABCD có:
A + B + C + D = 360 độ(theo định lý)
Suy ra C = 360 độ - ( A + B + D)
360 độ - 240 độ
120 độ
Vậy...
10 tháng 11 2021
a) \(\Leftrightarrow\left(3x+1\right)\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=1\end{matrix}\right.\)
b) \(\Leftrightarrow\left(2x-5\right)\left(2x+5\right)-\left(2x-5\right)\left(2x+7\right)=0\\ \Leftrightarrow\left(2x-5\right)\left(2x+5-2x-7\right)=0\\ \Leftrightarrow-2\left(2x-5\right)=0\\ \Leftrightarrow2x-5=0\\ \Leftrightarrow x=\dfrac{5}{2}\)
c) \(\Leftrightarrow2\left(x+3\right)-x\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(2-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)
d) \(\Leftrightarrow\left(x+3\right)\left(x^2-3x+9\right)+\left(x+3\right)\left(x-9\right)=0\\ \Leftrightarrow\left(x+3\right)\left(x^2-3x+9+x-9\right)=0\\ \Leftrightarrow\left(x+3\right)\left(x^2-2x\right)=0\\ \Leftrightarrow x\left(x+3\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=2\end{matrix}\right.\)
11 tháng 12 2021
b: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
Do đó: ADME là hình chữ nhật
AT
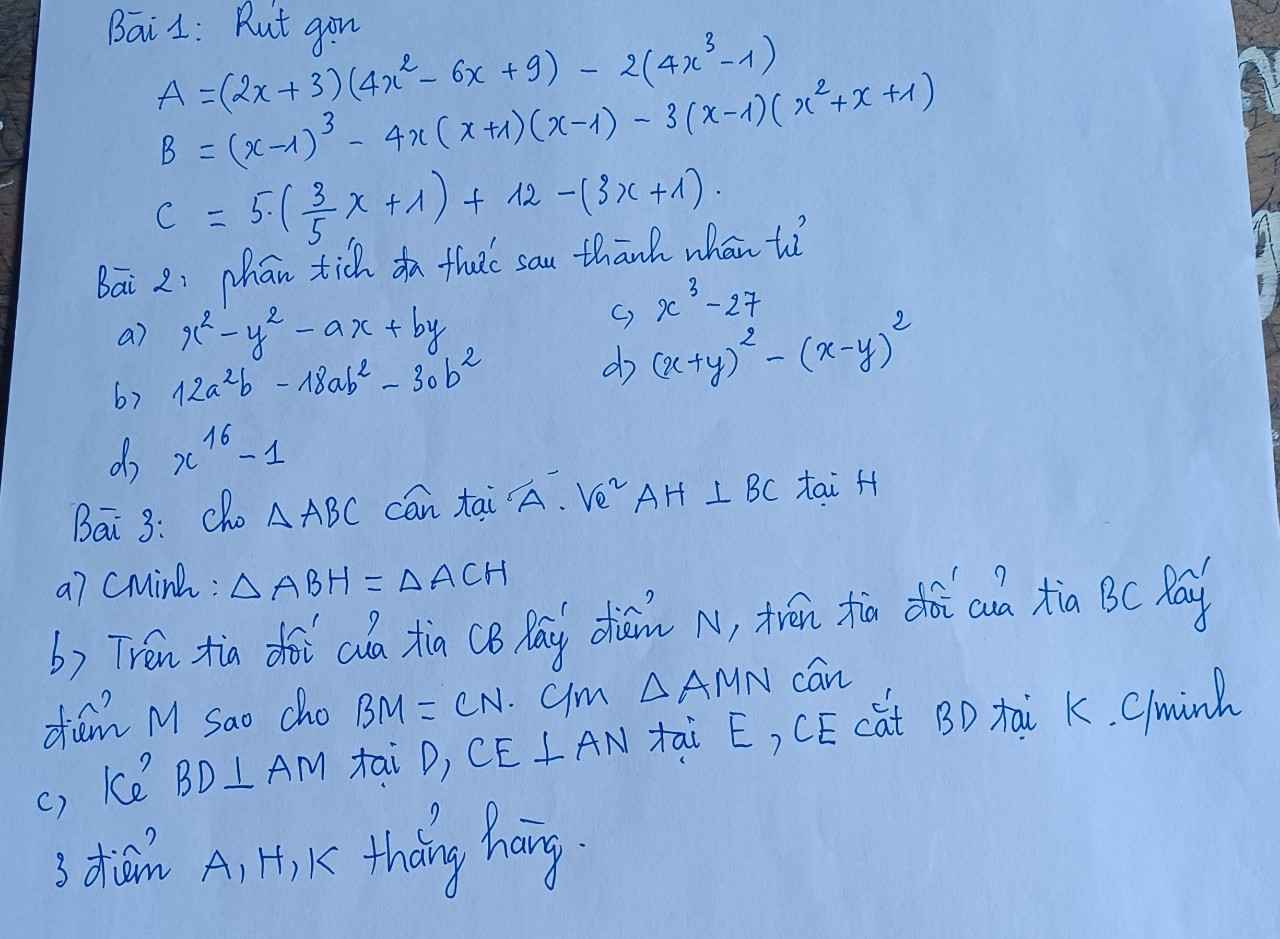
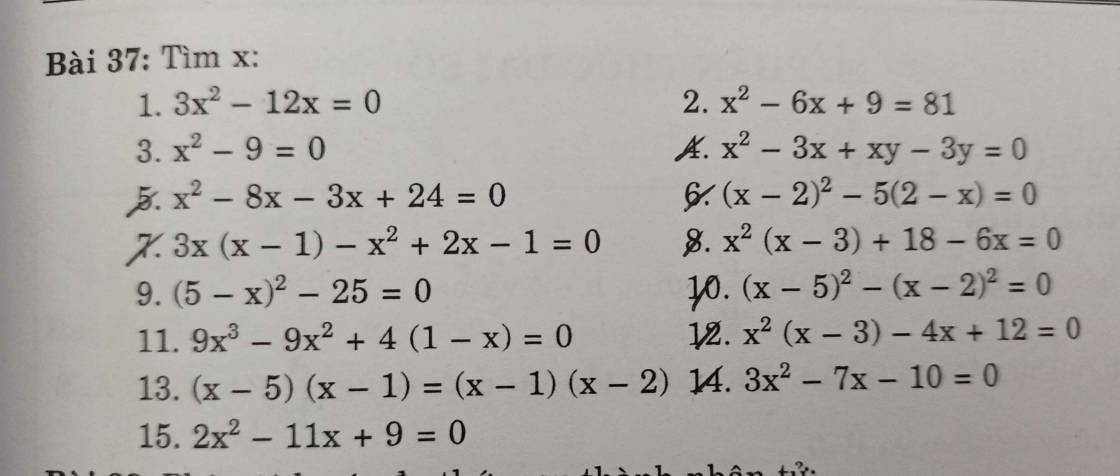
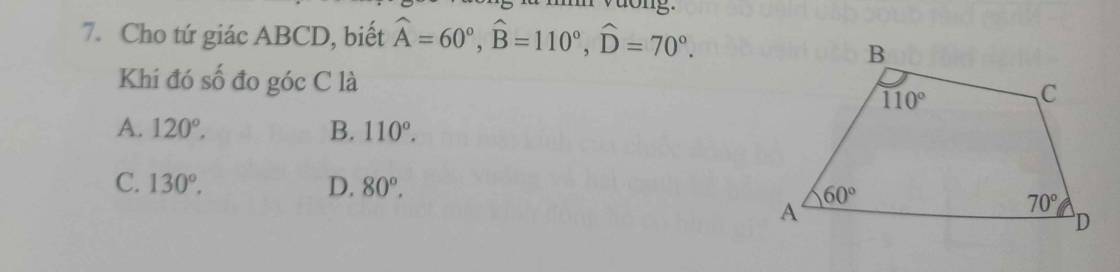
Ai giải hộ mình bài 18 với! Mình đang cần gấp lắm :(( Cảm ơn trước nha
1
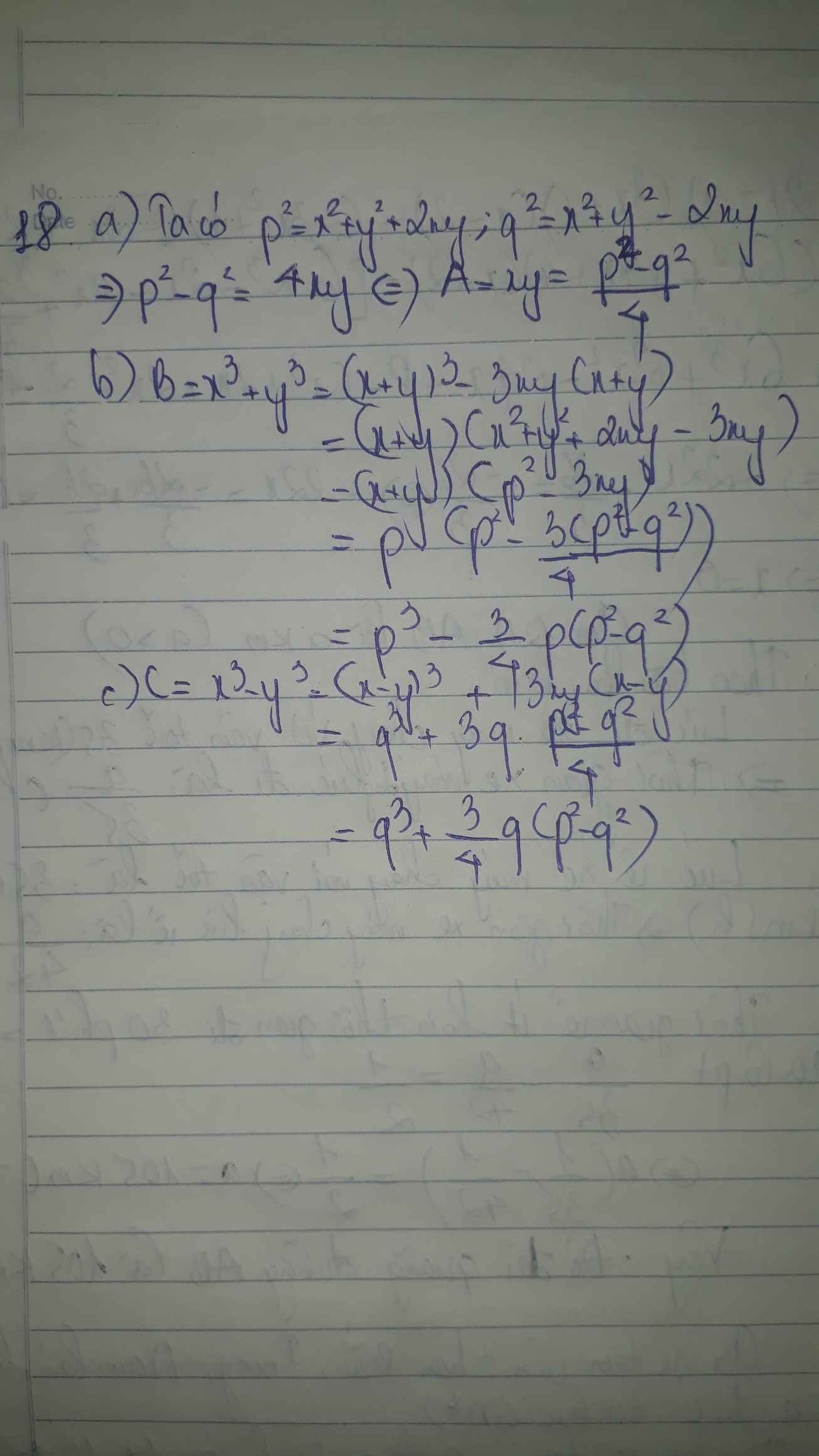
Bài 3:
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
b: Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)
\(\widehat{ACN}+\widehat{ACB}=180^0\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
Xét ΔAMN có AM=AN
nên ΔAMN cân tại A