DP
Giúp với ạ! Đang cần rất gấp ấy ạ! Giúp mình đi ạ!
7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 10 2021
Bài 1:
a) \(=\dfrac{\sqrt{5}.\sqrt{7}}{5}=\dfrac{\sqrt{35}}{5}\)
b) \(=\dfrac{\left|y\right|}{\sqrt{3}}=\dfrac{\sqrt{3}y}{3}\)
c) \(=\dfrac{\sqrt{2}}{\sqrt{t}}=\dfrac{\sqrt{2t}}{t}\)
d) \(=\sqrt{\dfrac{7p^2-3p^2}{7}}=\sqrt{\dfrac{4p^2}{7}}=\dfrac{2\left|p\right|}{\sqrt{7}}=\dfrac{-2\sqrt{7}p}{7}\)
Bài 2:
a) \(=\dfrac{\sqrt{21}-\sqrt{15}}{3}\)
b) \(=\dfrac{10\left(4+3\sqrt{2}\right)}{16-18}=-20-15\sqrt{2}\)
c) \(=\dfrac{\left(3\sqrt{10}-5\right)\left(6+\sqrt{10}\right)}{36-10}=\dfrac{18\sqrt{10}+30-30-5\sqrt{10}}{26}=\dfrac{13\sqrt{10}}{26}=\dfrac{\sqrt{10}}{2}\)
E
1
8 tháng 8 2021
ta có sinB=\(\dfrac{AH}{AB}\)\(\Rightarrow\)AH=AB.sinB=3,6.sin62=3,18
BH=\(\sqrt{AB^2-AH^2}\)(pytago)=\(\sqrt{3,6^2-3,18^2}\)=1,69
\(_{\widehat{C}}\)=90-\(\widehat{B}\)=90-62=28\(^0\)
sinC=\(\dfrac{AB}{BC}\)\(\Rightarrow\)BC=\(\dfrac{AB}{sinC}\)=\(\dfrac{3,6}{sin28}\)=7,67
mà:CH=BC-BH=7,67-1,69=5,98
AC=\(\sqrt{BC^2-AB^2}\)(pytago)=\(\sqrt{7,67^2-3,6^2}\)=6.77
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
b.
\(M=\sqrt{x}.\left[\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right].\frac{x-4}{2\sqrt{x}}\)
\(=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{2}=\frac{2\sqrt{x}}{x-4}.\frac{x-4}{2}=\sqrt{x}\)
c. Để $M>3\Leftrightarrow \sqrt{x}>3\Leftrightarrow x>9$
Kết hợp đkxđ suy ra $x>9$ thì $M>3$
26 tháng 9 2021
\(a,=2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{\left(\sqrt{5}-1\right)^2}}\\ =2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{5}-1}\\ =2\left(\sqrt{5}-1\right)\sqrt{6-2\sqrt{5}}\\ =2\left(\sqrt{5}-1\right)\sqrt{\left(\sqrt{5}-1\right)^2}\\ =2\left(\sqrt{5}-1\right)^2=2\left(6-2\sqrt{5}\right)=12-4\sqrt{5}\\ b,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)
TN
1
LD
6 tháng 4 2023
\(x^2-2\left(m-2\right)x+m^2+2m-3=0\left(1\right)\)
Để phương trình có hai nghiệm phân biệt thì Δ' > 0
\(\Rightarrow\left(m-2\right)^2-m^2-2m+3>0\Leftrightarrow m^2-4m+4-m^2-2m+3>0\Leftrightarrow-6m+7>0\Leftrightarrow m< \dfrac{7}{6}\)\)
Theo viét : \(\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-2\right)\\x_1x_2=m^2+2m-3\end{matrix}\right.\)\)
Lại có :\( \dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{5}\)
\(\Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}=\dfrac{x_1+x_2}{5}\)
\(\Rightarrow\left(x_1+x_2\right)\left(x_1x_2\right)=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(2m-4\right)\left(m^2+2m-3\right)=5\left(2m-4\right)\)
\(\Leftrightarrow2m^3+4m^2-6m-4m^2-8m+12=10m-20\)
\(\Leftrightarrow2m^3-24m+32=0\) \(\Leftrightarrow\left[{}\begin{matrix}m=-4\left(n\right)\\m=2\left(l\right)\end{matrix}\right.\)
Vậy \(m=-4\) thì thỏa điều kiện
NL
1
5 tháng 11 2021
Bài 5:
a: Xét ΔBEC và ΔADC có
\(\widehat{C}\) chung
\(\widehat{EBC}=\widehat{DAC}\)
Do đó: ΔBEC\(\sim\)ΔADC
HK
1
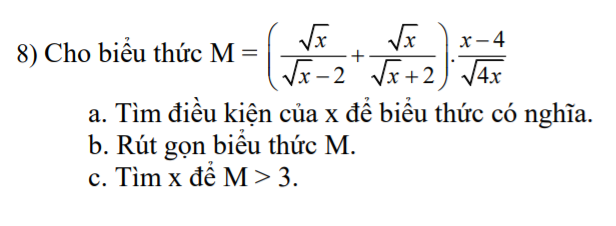
Mik có lớp 4 thôi seo giúp đc . Seo bn zô zuyên hế . ^~^
xin lỗi nhé