Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: =(x+y)^3+z^3-3xy(x+y)-3xyz
=(x+y+z)(x^2+2xy+y^2-xz-yz+z^2)-3xy(x+y+z)
=(x+y+z)(x^2+y^2+z^2-xy-xz-yz)
b: a+b+c<>0
A=(a+b+c)^3-a^3-b^3-c^3/a+b+c
=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)/(a+b+c)
=a^2+b^2+c^2-ab-ac-bc
=1/2[a^2-2ab+b^2+b^2-2bc+c^2+a^2-2ac+c^2]
=1/2[(a-b)^2+(b-c)^2+(a-c)^2]>=0

\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{2016}\)
\(\Rightarrow\dfrac{bc+ac+bc}{abc}=\dfrac{1}{2016}\)
\(\Rightarrow\dfrac{bc+ac+ab}{abc}=\dfrac{1}{a+b+c}\)
\(\Rightarrow\left(ab+bc+ca\right)\left(a+b+c\right)=abc\)
\(\Rightarrow ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+3abc=abc\)
\(\Rightarrow ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+2abc=0\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Rightarrow a=-b\) hay \(b=-c\) hay \(c=-a\)
-Vậy trong ba số a,b,c tồn tại 2 số đối nhau.

\(ab\left(a-b\right)+bc\left(b-c\right)+ca\left(c-a\right)\)
\(=ab\left(a-b\right)+bc\left(b-c\right)-ca\left(a-c\right)\)
\(=ab\left(a-b\right)+bc\left(b-c\right)-ca\left(a-b+b-c\right)\)
\(=ab\left(a-b\right)+bc\left(b-c\right)-ca\left(a-b\right)-ca\left(b-c\right)\)
\(=\left(a-b\right)\left(ab-ca\right)+\left(b-c\right)\left(bc-ca\right)\)
\(=\left(a-b\right)a\left(b-c\right)+\left(b-c\right)c\left(b-a\right)\)
\(=\left(a-b\right)a\left(b-c\right)-\left(b-c\right)c\left(a-b\right)\)
\(=\left(a-b\right)\left(b-c\right)\left(a-c\right)\)
mình làm vội, có chỗ nào sai bạn thông cảm nha
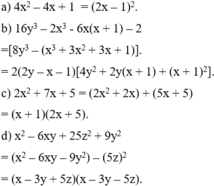
 k cho tui nha
k cho tui nha
2. Ta có : \(\hept{\begin{cases}a+b+c=2016\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{2016}\end{cases}\Leftrightarrow}\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\)
\(\Leftrightarrow\left(\frac{1}{a}+\frac{1}{b}\right)+\left(\frac{1}{c}-\frac{1}{a+b+c}\right)=0\Leftrightarrow\frac{a+b}{ab}+\frac{a+b}{c\left(a+b+c\right)}=0\)
\(\Leftrightarrow\left(a+b\right)\left(ab+ac+bc+c^2\right)=0\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Leftrightarrow a+b=0\) hoặc \(b+c=0\) hoặc \(a+c=0\)
Từ (1) , (2) , (3) ta có điều phải chứng minh.