Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
b: Xét ΔBDC vuông tại B có BH là đường cao
nên \(HC\cdot HD=BH^2\left(1\right)\)
Xét ΔBHC vuông tại H có HE là đường cao
nên \(BE\cdot BC=BH^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HD=BE\cdot BC\)


a) \(\left\{{}\begin{matrix}mx+y=1.\\x+my=m+1.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-mx.\\x+m\left(1-mx\right)=m+1.\left(1\right)\end{matrix}\right.\)
Xét (1): \(x+m\left(1-mx\right)=m+1.\Leftrightarrow x+m-m^2x-m-1=0.\Leftrightarrow\left(1-m^2\right)x-1=0.\left(2\right)\)
Để hệ phương trình có nghiệm duy nhất. \(\Leftrightarrow\) (2) có nghiệm duy nhất.
\(\Leftrightarrow1-m^2\ne0.\Leftrightarrow m^2\ne1.\Leftrightarrow m\ne\pm1.\)
b) Để hệ phương trình có vô số nghiệm. \(\Leftrightarrow\) (2) có vô số nghiệm.
\(\Leftrightarrow\left\{{}\begin{matrix}1-m^2=0.\\-1=0.\end{matrix}\right.\) (vô lý).
\(\Rightarrow m\in\phi\).
c) Để hệ phương trình có vô nghiệm. \(\Leftrightarrow\) (2) có vô nghiệm.
\(\Leftrightarrow\left\{{}\begin{matrix}1-m^2=0.\\-1\ne0.\end{matrix}\right.\)\(\Leftrightarrow1-m^2=0.\Leftrightarrow m^2=1.\Leftrightarrow m=\pm1.\)

Câu 1:
1: Ta có: \(A=3\sqrt{25}-\sqrt{36}-\sqrt{64}\)
\(=3\cdot5-6-8\)
\(=15-6-8=1\)
Câu I:
2: Ta có: \(B=\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{x+1}{x-1}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{x+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-\sqrt{x}+x+\sqrt{x}-x-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-1}{x-1}=1\)

\(A=\dfrac{x+y+2\sqrt{xy}}{\sqrt{x}+\sqrt{y}}-\dfrac{x-y}{\sqrt{x}+\sqrt{y}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{\sqrt{x}+\sqrt{y}}-\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}=\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\)
\(=2\sqrt{y}\)
\(B=\dfrac{x+y-2\sqrt{xy}}{\sqrt{x}-\sqrt{y}}-\dfrac{x-y}{\sqrt{x}+\sqrt{y}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{x}-\sqrt{y}}-\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}=\left(\sqrt{x}-\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\)
\(=0\)
\(C=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+4\sqrt{xy}}{\sqrt{x}+\sqrt{y}}+\dfrac{x\sqrt{y}+y\sqrt{x}}{\sqrt{x}\sqrt{y}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{\sqrt{x}+\sqrt{y}}+\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}=\sqrt{x}+\sqrt{y}+\sqrt{x}+\sqrt{y}\)
\(=2\left(\sqrt{x}+\sqrt{y}\right)\)
\(D=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2-4\sqrt{xy}}{\sqrt{x}-\sqrt{y}}+\dfrac{y\sqrt{x}-x\sqrt{y}}{\sqrt{xy}}\left(x,y>0\right)\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{x}-\sqrt{y}}+\dfrac{\sqrt{xy}\left(\sqrt{y}-\sqrt{x}\right)}{\sqrt{xy}}=\sqrt{x}-\sqrt{y}+\sqrt{y}-\sqrt{x}=0\)

Câu 4:
1: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=\left(20a\right)^2+\left(21a\right)^2=841a^2\)
=>\(BC=\sqrt{841a^2}=29a\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH\cdot29a=\left(20a\right)^2=400a^2\)
=>\(BH=\dfrac{400}{29}a\)
2: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
=>\(tanBAM=tanABM=tanABC=\dfrac{AC}{AB}=\dfrac{21}{20}\)
Câu 5:
1: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>BD\(\perp\)DA tại D
=>BD\(\perp\)AC tại D
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE\(\perp\)EB tại E
=>AE\(\perp\)BC tại E
Xét ΔCAB có
AE,BD là các đường cao
AE cắt BD tại H
Do đó: H là trực tâm của ΔCAB
=>CH\(\perp\)AB
2:
Gọi giao điểm của CH với AB là K
=>CH\(\perp\)AB tại K
Ta có: ΔCDH vuông tại D
mà DF là đường trung tuyến
nên FH=FD=FC
\(\widehat{FDO}=\widehat{FDH}+\widehat{ODB}\)
\(=\widehat{OBD}+\widehat{FHD}\)
\(=\widehat{KHB}+\widehat{KBH}=90^0\)
=>FD\(\perp\)DO tại D
=>FD là tiếp tuyến của (O)

Bài 2:
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp


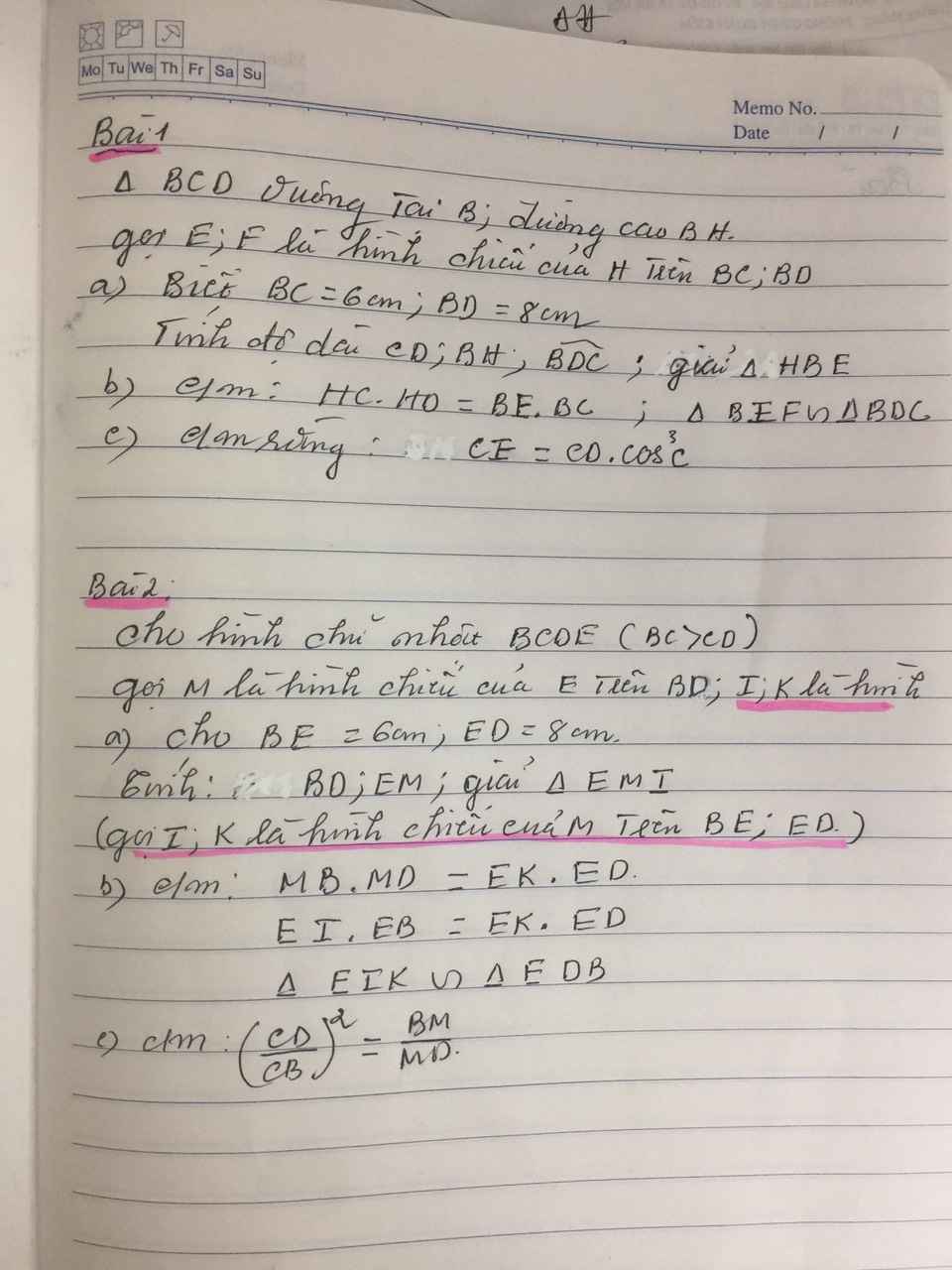



 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 

 Giúp tớ câu 4 hoặc câu 5 với ạ
Giúp tớ câu 4 hoặc câu 5 với ạ không cần làm câu c đâu ạ, giúp e với nhaaa mn
không cần làm câu c đâu ạ, giúp e với nhaaa mn