Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BẠn vẽ hình nha
đề của bạn có xíu vần đề nhưng mk cx hiểu đc oy nếu có nhầm đỉnh bạn sửa nha
Dễ c/m được tứ giác SPAM nội tiếp( do SMA=SPA =90)
nên ta được PMA=PSA (cùng chắn cung PA)
Áp dụng định lý ta lét , ta có:
\(\frac{MF}{PS}=\frac{BW}{PB}=\frac{WM}{PS'}\Rightarrow PS=PS'\)
nên SAS' cân tại A hay ASS'=AS'S
nên ta có : PMS'=PS'M hay S'P=PM
OP là trung trực của MM' nên PM=PM'
nên S'P=PM' hay PS'M' cân tại P
b)
Dễ thấy :
PSM=SMP và OMB=OBM
mà PSM+MBO=90
nên PMS+OMB=90
nên PMO=90
hay PM là tiếp tuyến của (O)
Chúc bạn học tốt nha ^-^
a) Do AMNP là hình vuông nên \(\widehat{QMB}=45^o\)
Lại có do C là điểm chính giữa của nửa đường tròn nên \(\widebat{CB}=90^o\Rightarrow\widehat{CMB}=45^o\)
(Góc nội tiếp)
Vậy thì \(\widehat{CMQ}=\widehat{CMB}+\widehat{BMQ}=45^o+45^o=90^o\)
Vậy CQ là đường kính hay C và Q đối xứng nhau qua O.
b) Ta thấyAMNP là hình vuông. MI là phân giác góc \(\widehat{AMB}\) nên \(\Delta MAI=\Delta MNI\left(c-g-c\right)\Rightarrow\widehat{MAI}=\widehat{MNI}\)
Lại có \(\widehat{MAI}=\widehat{IAM}\) nên \(\widehat{MNI}=\widehat{IAM}\)
Xét tứ giác AINB có \(\widehat{MNI}=\widehat{IAM}\) nên AINB là tứ giác nội tiếp (góc ngoài tại đỉnh bằng góc đối diện)
a) ˆAEB=90oAEB^=90o (góc nội tiếp chắn nửa đường tròn) ⇒BE⊥AE⇒BE⊥AE mà CM⊥AECM⊥AE (giả thiết)
⇒BE∥CM⇒ˆCME=ˆMEB⇒BE∥CM⇒CME^=MEB^ (hai góc ở vị trí so le trong)
Mà ˆMCB=ˆMEBMCB^=MEB^ (góc nội tiếp cùng chắn cung MB)
⇒ˆCME=ˆMCB⇒CME^=MCB^ (=ˆMEB)(=MEB^)
⇒⇒ cung CE = cung MB
mà cung MB=cung AM (do M là điểm chính giữa của cung AB)
⇒⇒ cung AM=AM= cung CE⇒AM=CECE⇒AM=CE (1) và
ˆACM=ˆCMEACM^=CME^ (góc nội tiếp cùng chắn 2 cung bằng nhau cung AM=cung CE) mà chúng ở vị trí so le trong nên AC//ME⇒ACEMAC//ME⇒ACEM là hình thang lại có thêm AM=CE (cmt) ⇒ACEM⇒ACEM là hình thang cân
b) Do M là điểm chính giữa của cung AB nên MO⊥ABMO⊥AB
CH⊥ABCH⊥AB (giả thiết)
⇒MO//CH⇒ˆHCM=ˆCMO⇒MO//CH⇒HCM^=CMO^ (hai góc ở vị trí so le trong) (2)
ΔOCMΔOCM cân đỉnh O (OM=OC=R) ⇒ˆMCO=ˆCMO⇒MCO^=CMO^ (3)
Từ (2) và (3) suy ra ˆHCM=ˆMCOHCM^=MCO^
⇒CM⇒CM là phân giác của ˆHCOHCO^ (đpcm)
a) ˆAEB=90oAEB^=90o (góc nội tiếp chắn nửa đường tròn) ⇒BE⊥AE⇒BE⊥AE mà CM⊥AECM⊥AE (giả thiết)
⇒BE∥CM⇒ˆCME=ˆMEB⇒BE∥CM⇒CME^=MEB^ (hai góc ở vị trí so le trong)
Mà ˆMCB=ˆMEBMCB^=MEB^ (góc nội tiếp cùng chắn cung MB)
⇒ˆCME=ˆMCB⇒CME^=MCB^ (=ˆMEB)(=MEB^)
⇒⇒ cung CE = cung MB
mà cung MB=cung AM (do M là điểm chính giữa của cung AB)
⇒⇒ cung AM=AM= cung CE⇒AM=CECE⇒AM=CE (1) và
ˆACM=ˆCMEACM^=CME^ (góc nội tiếp cùng chắn 2 cung bằng nhau cung AM=cung CE) mà chúng ở vị trí so le trong nên AC//ME⇒ACEMAC//ME⇒ACEM là hình thang lại có thêm AM=CE (cmt) ⇒ACEM⇒ACEM là hình thang cân
b) Do M là điểm chính giữa của cung AB nên MO⊥ABMO⊥AB
CH⊥ABCH⊥AB (giả thiết)
⇒MO//CH⇒ˆHCM=ˆCMO⇒MO//CH⇒HCM^=CMO^ (hai góc ở vị trí so le trong) (2)
ΔOCMΔOCM cân đỉnh O (OM=OC=R) ⇒ˆMCO=ˆCMO⇒MCO^=CMO^ (3)
Từ (2) và (3) suy ra ˆHCM=ˆMCOHCM^=MCO^
⇒CM⇒CM là phân giác của ˆHCOHCO^ (đpcm)
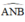là góc nội tiếp chắn nửa đường tròn ⇒ 
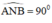⇒ AN ⊥ NB
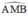là góc nội tiếp chắn nửa đường tròn ⇒ 
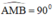⇒ AM ⊥ MB
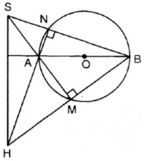
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)
Kiến thức áp dụng
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Trong một tam giác, ba đường cao đồng quy tại trực tâm.