Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

△ABH∼△CAH (g-g) \(\Rightarrow\dfrac{P_{ABH}}{P_{CAH}}=\dfrac{AB}{CA}=\dfrac{18}{24}=\dfrac{3}{4}\)
\(\Rightarrow AB=\dfrac{3}{4}CA\)
△ABC vuông tại A có: \(BC^2=AB^2+AC^2\Rightarrow BC^2=\dfrac{9}{16}CA^2+CA^2=\dfrac{25}{16}CA^2\)
\(\Rightarrow BC=\dfrac{5}{4}CA\)
△CAH∼△CBA (g-g) \(\Rightarrow\dfrac{P_{CAH}}{P_{CBA}}=\dfrac{CA}{CB}=\dfrac{CA}{\dfrac{5}{4}CA}=\dfrac{4}{5}\)
\(\Rightarrow P_{CBA}=\dfrac{5}{4}.P_{CAH}=\dfrac{5}{4}.24=30\left(cm\right)\)

Không mất tính tổng quát
g/s: BH=9m , CH=16m
Ta có: BC=BH+HC=25m
Xét tam giác ABC vuông tại A
=> \(AB^2+AC^2=BC^2=625\)
Xét tam giác ABH và ACH vuông tại H có: \(AB^2=AH^2+BH^2=AC^2-CH^2+BH^2\)=> \(AB^2=AC^2-16^2+9^2=AC^2-175\)
=> \(AC^2-175+AC^2=625\Rightarrow AC^2=400\Rightarrow AC=20\)m
=> \(AB^2=AC^2-175=225\Rightarrow AC=15\)m
Chu vi= 15+20+25=60 m

Xét △AHB và △CHA có:
\(\widehat{AHB}=\widehat{CAB}=90^o\)
\(\widehat{ABH}=\widehat{CAH}\)(cùng phụ \(\widehat{HAB}\))
=> △AHB đồng dạng với △CHA (g.g)
=> \(\frac{AH}{CH}=\frac{AB}{CA}=\frac{AH+AB+HB}{CH+CA+HA}=\frac{18}{24}=\frac{3}{4}\left(1\right)\)
Xét △AHB và △CAB ta có:
\(\widehat{AHB}=\widehat{CAB}=90^o\)
\(\widehat{B}\)là góc chung
=> △AHB đồng dạng với △CAB (g.g)
=> \(\frac{AH}{CA}=\frac{AB}{CB}=\frac{AH+AB+HB}{CA+CB+AB}=\frac{18}{CA+CB+AB}\left(2\right)\)
Từ (1) ta đặt AB=3k, CA=4k. Xét △ABC vuông tại A
CB2=AB2+CA2=(3k)2+(4k)2=(5k)2
nên CB=5k. Do đó: \(\frac{AB}{CB}=\frac{3}{5}\)
Từ (2) => \(\frac{3}{5}=\frac{18}{P_{\text{△}ABC}}\)
Vậy \(P_{\text{△}ABC}=18\cdot\frac{5}{3}=30\left(cm\right)\)
Gọi \(P_1,P_2,P_3\) lần lượt là chu vi của tam giác \(AHB;AHC;ABC\) ;
\(\Delta AHB\infty\Delta CHA\)suy ra
\(\frac{P_1}{P_2}=\frac{AB}{CA}\) (1)
Từ (1) , ta có:
\(\frac{AB}{AC}=\frac{18}{24}=\frac{3}{4}\Rightarrow\frac{AB}{3}=\frac{AC}{4}\)
\(\Leftrightarrow\frac{AB^2}{3^2}=\frac{AC^2}{4^2}=\frac{AB^2+AC^2}{3^2+4^2}=\frac{BC^2}{5^2}\)
\(\Leftrightarrow\frac{AB}{3}=\frac{AC}{4}=\frac{BC}{5}\Rightarrow AB:AC:BC=3:4:5\)
\(P_1:P_2:P_3=AB:AC:BC=3:4:5\)
Vậy nếu \(P_1=18cm,\) ,\(P_2=24cm\) thì \(P_3=30cm\) .

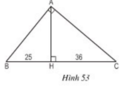
+ BC = BH + HC = 25 + 36 = 61 (cm)
+ ΔABH vuông tại H và ΔABC vuông tại A có:
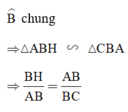
⇒AB2=BH.BC=25.(25+36)=1525


Ta có: \(\dfrac{MB}{MC}=\dfrac{1}{2}\)(gt)
nên MC=2MB
Ta có: MB+MC=BC(M nằm giữa B và C)
nên BC=2MB+MB=3MB
hay \(\dfrac{MB}{BC}=\dfrac{1}{3}\)
Xét ΔABC có
M∈BC(gt)
D∈AB(gt)
MD//AC(gt)
Do đó: ΔBMD\(\sim\)ΔBCA(Định lí tam giác đồng dạng)
⇒\(\dfrac{C_{BMD}}{C_{BCA}}=\dfrac{BM}{BC}\)(Tỉ số chu vi giữa hai tam giác đồng dạng)
\(\Leftrightarrow\dfrac{C_{BMD}}{24}=\dfrac{1}{3}\)
hay \(C_{DBM}=8\left(cm\right)\)
Ta có: \(\dfrac{MB}{MC}=\dfrac{1}{2}\)(gt)
nên \(MB=\dfrac{1}{2}MC\)
Ta có: MB+MC=BC(M nằm giữa B và C)
nên \(BC=\dfrac{1}{2}MC+MC=\dfrac{3}{2}MC\)
hay \(\dfrac{MC}{BC}=\dfrac{2}{3}\)
Xét ΔCBA có
M∈BC(gt)
E∈CA(Gt)
ME//AB(gt)
Do đó: ΔCME∼ΔCBA(Định lí tam giác đồng dạng)
\(\Leftrightarrow\dfrac{C_{CME}}{C_{CBA}}=\dfrac{CM}{CB}\)(Tỉ số chu vi giữa hai tam giác đồng dạng)
⇔\(\dfrac{C_{CME}}{24}=\dfrac{2}{3}\)
hay \(C_{CME}=\dfrac{48}{3}=16\left(cm\right)\)
Vậy: \(C_{DBM}=8\left(cm\right)\); \(C_{CME}=16\left(cm\right)\)

Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~