K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 7 2023
5:
a: Vì (d1)//(d) nên a=2
=>y=2x+b
Khi x=2 thì y=-1/2*2^2=-2
Thay x=2 và y=-2 vào (d1), ta được;
b+4=-2
=>b=-6
b: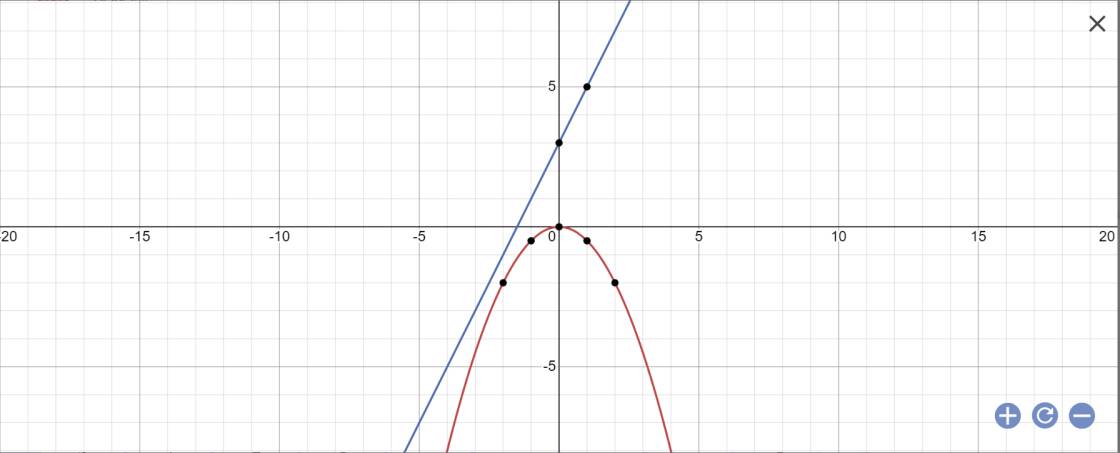 
6 tháng 1 2022
b: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
Xét tứ giác AEIF có
\(\widehat{AEI}+\widehat{AFI}=180^0\)
Do đó: AEIF là tứ giác nội tiếp
giải giúp mấy bài này đi mấy bạn
28 tháng 6 2021
â)ĐK;`x-2>=0`
`<=>x>=2`
c)ĐK:`2017/x>=0(x ne 0)`
Mà `2017>0`
`<=>x>0`
e)ĐK:`x^2+2017>=0`
`<=>x^2>=-2017AAx in RR`
b)ĐK:`2-3x>=0`
`<=>3x<=2`
`<=>x<=2/3`
d)ĐK:`(-2017)/(5-x)>=0(x ne 5)`
`<=>2017/(x-5)>=0`
Mà `2017>0`
`<=>x-5>0<=>x>5`
f)ĐK:`1-x^2>=0`
`<=>x^2<=1`
`<=>-1<=x<=1`
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2022
Đề bài ko chính xác, nếu x bất kì thì tồn tại vô số x để P nguyên
Nếu \(x\) nguyên thì mới có hữu hạn giá trị x
21 tháng 8 2021
Bài 1:
a: Xét tứ giác NPIK có
\(\widehat{NKP}=\widehat{NIP}\left(=90^0\right)\)
Do đó: NPIK là tứ giác nội tiếp
hay N,P,I,K cùng thuộc 1 đường tròn
b: Xét tứ giác MKHI có
\(\widehat{MKH}+\widehat{MIH}=180^0\)
Do đó: MKHI là tứ giác nội tiếp
hay M,K,H,I cùng thuộc 1 đường tròn
AT
28 tháng 7 2021
\(B=\left(3+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(3-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(a\ge0,a\ne1\right)\)
\(=\left(3+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(3-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)=\left(3+\sqrt{a}\right)\left(3-\sqrt{a}\right)=9-a\)
Để hàm số \(y=\left(m-1\right)x+2\) đồng biến trên R thì \(m-1>0\Rightarrow m>1\)
28 tháng 7 2021
Câu 2:
Để hàm số y=(m-1)x+2 đồng biến trên R thì m-1>0
hay m>1
AT
12 tháng 7 2021
a) \(\left\{{}\begin{matrix}2x-3y=11\\5x-4y=3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}10x-15y=55\left(1\right)\\10x-8y=6\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)-\left(2\right)\Rightarrow-7y=49\Rightarrow y=-7\Rightarrow2x=11+3\left(-7\right)=-10\)
\(\Rightarrow x=-5\)
b) đề nãy chỉ có 1 pt x,y không thể tính x,y được
c) bạn viết đề rõ ra chứ mờ quá đọc ko được
1 tháng 11 2021
\(a,=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}\left(\sqrt{5}-\sqrt{2}\right)}=\dfrac{\sqrt{21}}{7}\\ b,=\dfrac{\sqrt{5}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{4}\left(\sqrt{3}+\sqrt{2}\right)}=\dfrac{\sqrt{5}}{2}\\ c,=\dfrac{\sqrt{x}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{\sqrt{xy}}{y}\\ d,=\dfrac{\left(\sqrt{3}-\sqrt{2}\right)\left(2\sqrt{5}-\sqrt{3}\right)}{\left(2\sqrt{5}-\sqrt{3}\right)\left(1-\sqrt{2}\right)}=\dfrac{\sqrt{3}-\sqrt{2}}{1-\sqrt{2}}\\ =\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}+1\right)=2+\sqrt{2}-\sqrt{6}+\sqrt{3}\)
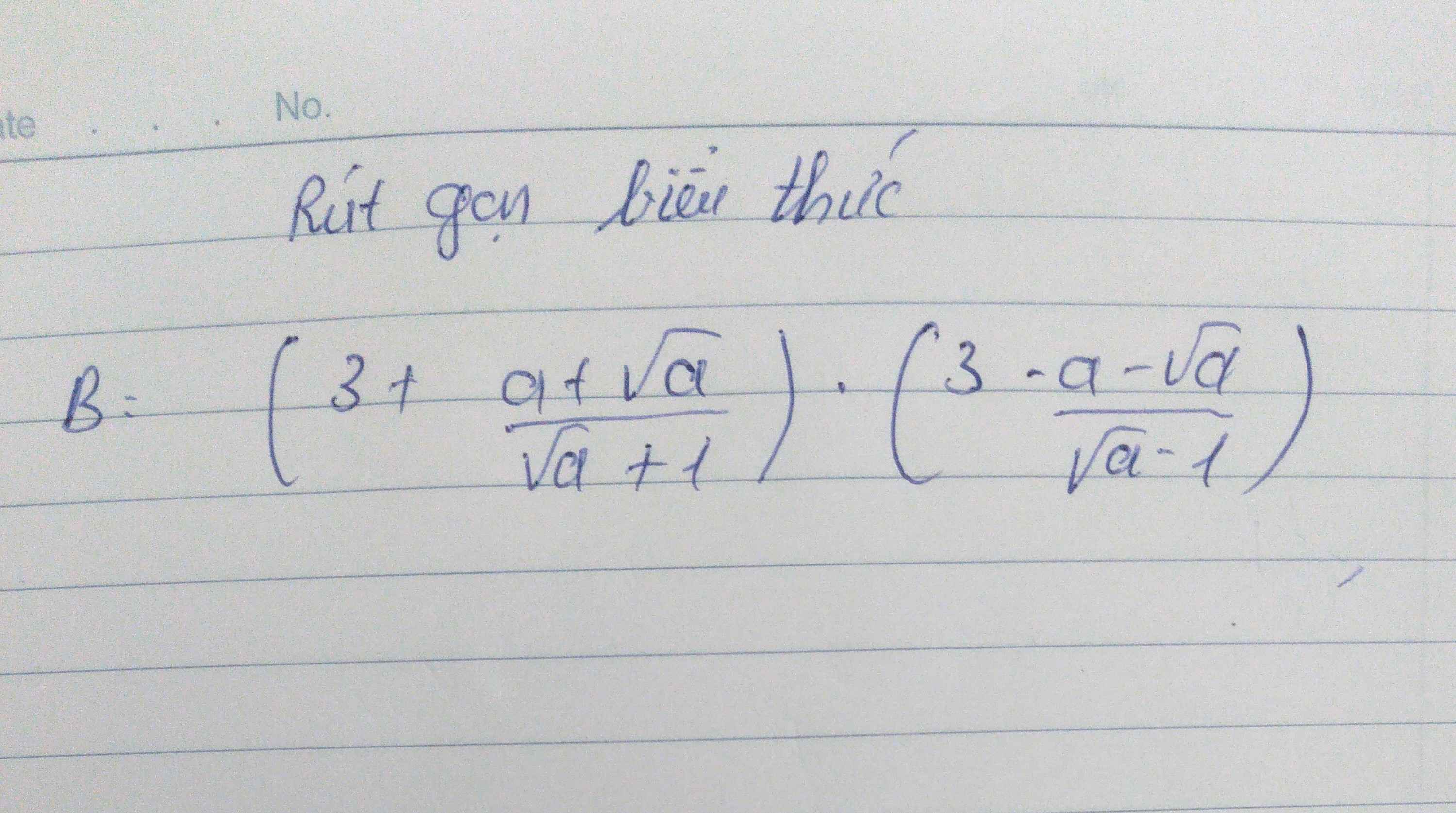
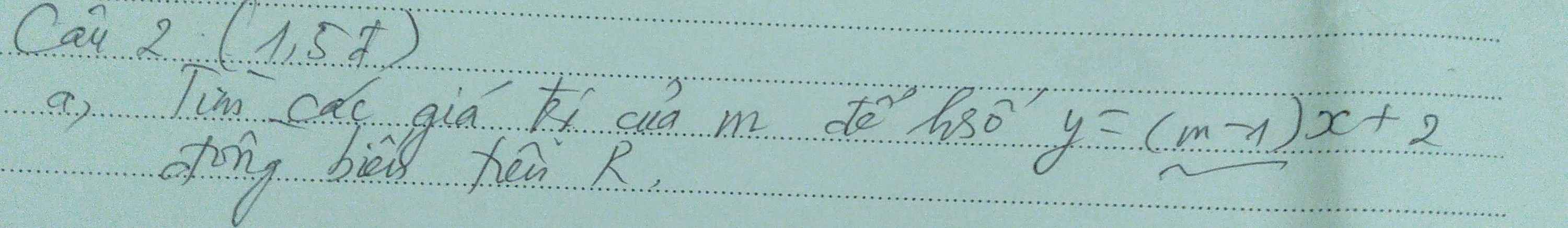
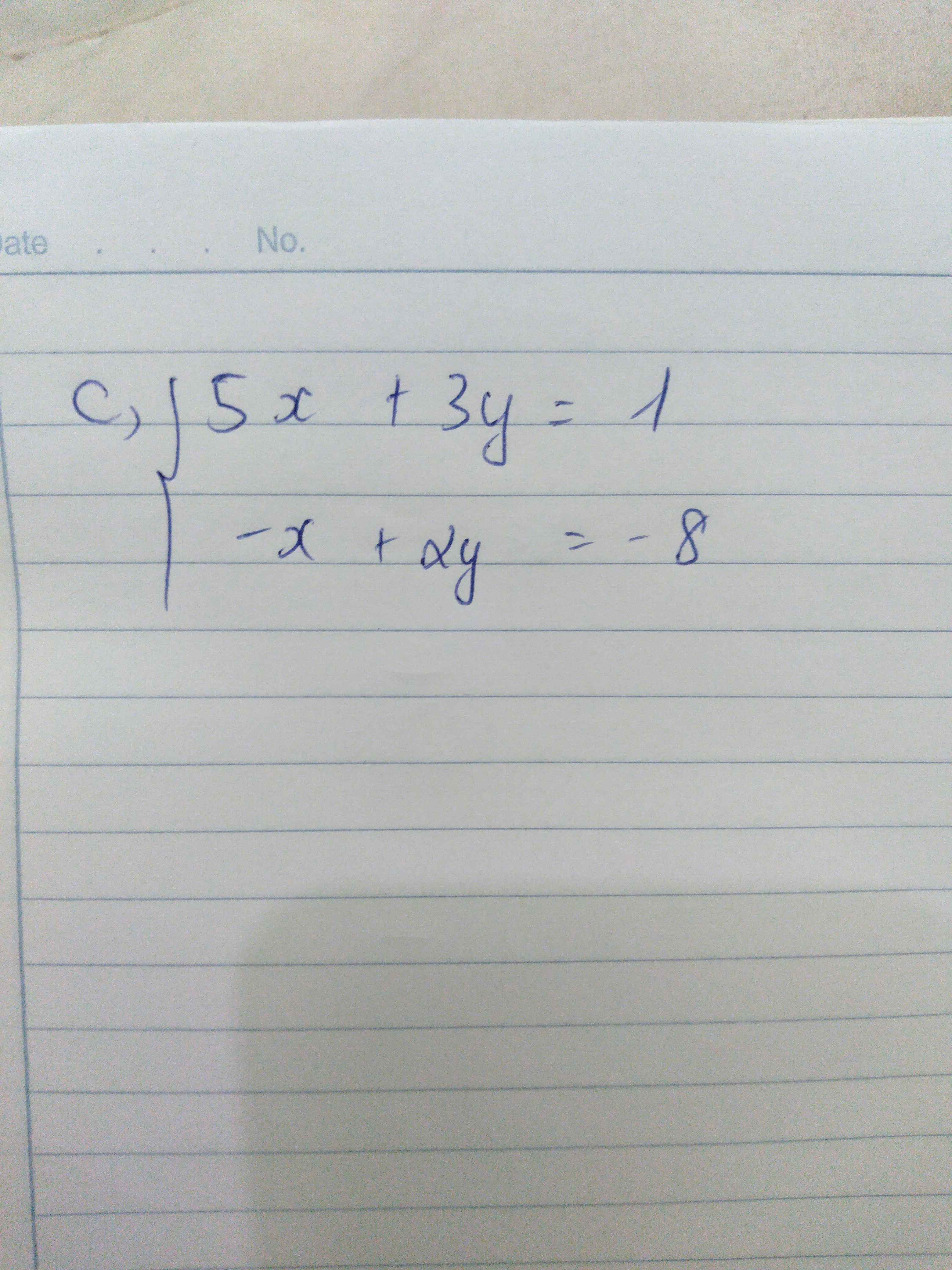
a: \(\sqrt{10}\cdot\sqrt{40}=\sqrt{400}=20\)
b: \(\sqrt{5}\cdot\sqrt{45}=\sqrt{225}=15\)
c: \(\sqrt{52}\cdot\sqrt{13}=\sqrt{676}=26\)
d: \(\sqrt{2}\cdot\sqrt{162}=\sqrt{324}=18\)