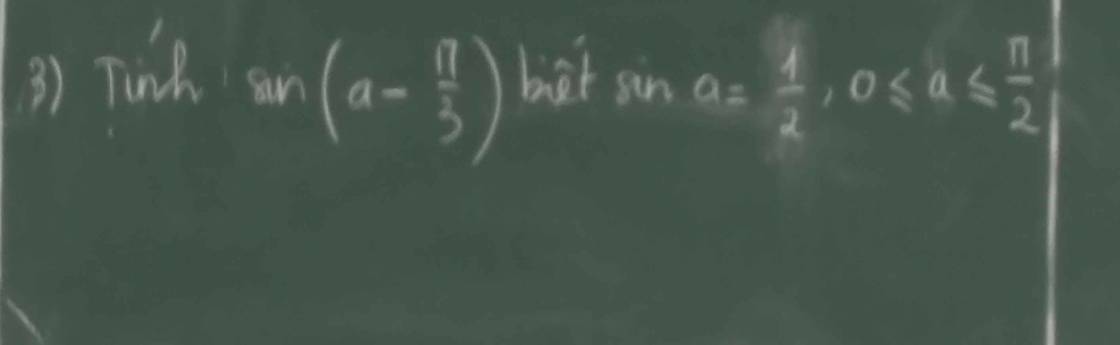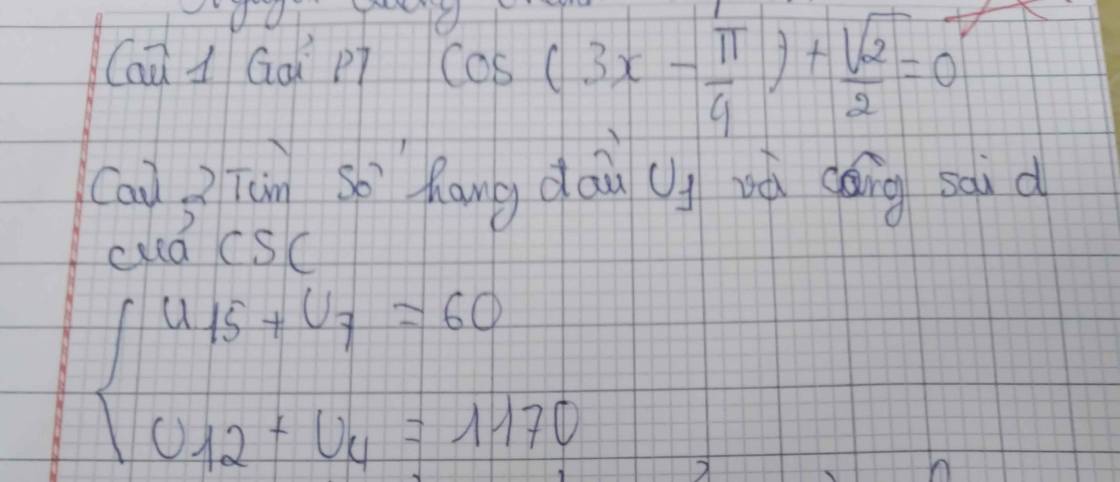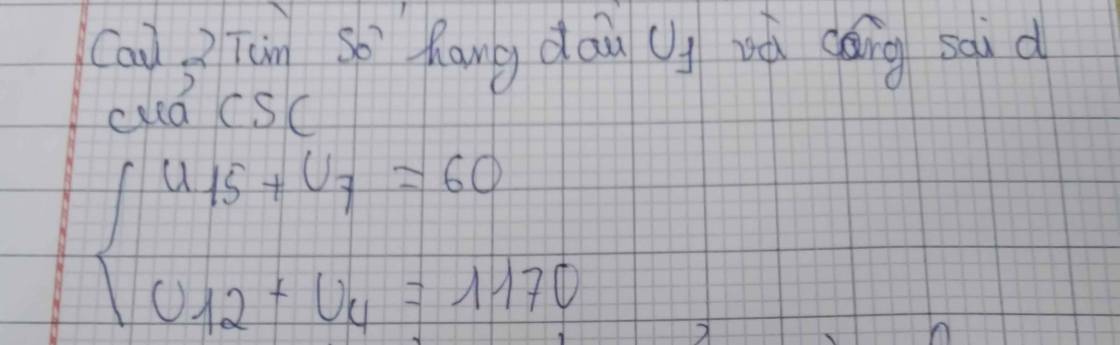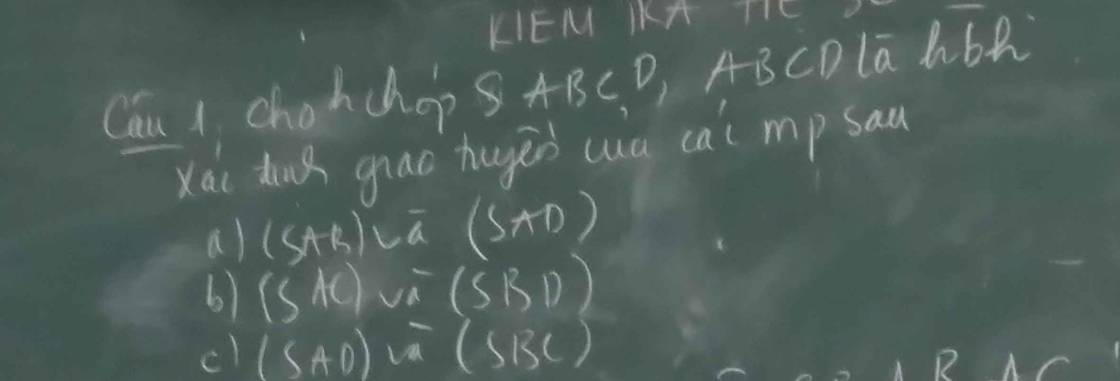TK
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
0
TV
2
TA
4 tháng 7 2021
ĐK: `x \ne kπ`
`cot(x-π/4)+cot(π/2-x)=0`
`<=>cot(x-π/4)=-cot(π/2-x)`
`<=>cot(x-π/4)=cot(x-π/2)`
`<=> x-π/4=x-π/2+kπ`
`<=>0x=-π/4+kπ` (VN)
Vậy PTVN.
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
\(f'\left(x\right)=x^2+2x\)
a.
\(f'\left(-3\right)=3\) ; \(f\left(-3\right)=-2\)
Phương trình tiếp tuyến:
\(y=3\left(x+3\right)-2\Leftrightarrow y=3x+7\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm, do hệ số góc tiếp tuyến bằng 3
\(\Rightarrow f'\left(x_0\right)=3\Rightarrow x_0^2+2x_0=3\Rightarrow x_0^2+2x_0-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=1\Rightarrow y_0=-\dfrac{2}{3}\\x_0=-3\Rightarrow y_0=-2\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=3\left(x-1\right)-\dfrac{2}{3}=3x-\dfrac{11}{3}\\y=3\left(x+3\right)-2=3x+7\end{matrix}\right.\)
c. Tiếp tuyến song song (d) nên có hệ số góc bằng 8
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow x_0^2+2x_0=8\)
\(\Rightarrow\left[{}\begin{matrix}x_0=2\Rightarrow y_0=\dfrac{14}{3}\\x_0=-4\Rightarrow y_0=-\dfrac{22}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=8\left(x-2\right)+\dfrac{14}{3}=...\\y=8\left(x+4\right)-\dfrac{22}{3}=...\end{matrix}\right.\)
DV
1
8 tháng 9 2023
\(sina=\dfrac{1}{2}\left(0\le a\le\dfrac{\pi}{2}\right)\)
\(sin^2a+cos^2a=1\)
\(\Rightarrow cos^2a=1-sin^2a=1-\dfrac{1}{4}=\dfrac{3}{4}\)
\(\Rightarrow cosa=\dfrac{\sqrt[]{3}}{2}\) \(\left(0\le a\le\dfrac{\pi}{2}\Rightarrow cosa>0\right)\)
\(sin\left(a-\dfrac{\pi}{3}\right)\)
\(=sina.cos\dfrac{\pi}{3}+cosa.sin\dfrac{\pi}{3}\)
\(\)\(=\dfrac{1}{2}.\dfrac{1}{2}+\dfrac{\sqrt[]{3}}{2}.\dfrac{\sqrt[]{3}}{2}\)
\(\)\(=\dfrac{1}{4}+\dfrac{3}{4}=1\)
DV
1
11 tháng 10 2023
2:
\(\Leftrightarrow\left\{{}\begin{matrix}u1+14d+u1+6d=60\\u1+11d+u1+3d=1170\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2u1+20d=60\\2u1+14d=1170\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6d=-1110\\u1+10d=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=-185\\u1=30-10d=1880\end{matrix}\right.\)
1:
\(PT\Leftrightarrow cos\left(3x-\dfrac{pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\)
=>\(\left[{}\begin{matrix}3x-\dfrac{\Omega}{4}=\dfrac{3}{4}\Omega+k2\Omega\\3x-\dfrac{\Omega}{4}=-\dfrac{3}{4}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=\Omega+k2\Omega\\3x=-\dfrac{1}{2}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{3}+\dfrac{k2\Omega}{3}\\x=-\dfrac{1}{6}\Omega+\dfrac{k2\Omega}{3}\end{matrix}\right.\)
DV
1
11 tháng 10 2023
Ta có :
\(\left\{{}\begin{matrix}u_{15}+u_7=60\\u_{12}+u_4=1170\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+14d+u_1+6d=60\\u_1+11d+u_1+3d=1170\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2u_1+20d=60\\2u_1+14d=1170\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-6d=1110\\2u_1+20d=60\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}d=-185\\u_1=30-10d\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}d=-185\\u_1=1880\end{matrix}\right.\)
14 tháng 11 2023
a:
Ta có: \(SA\subset\left(SAB\right)\)
\(SA\subset\left(SAD\right)\)
Do đó: \(\left(SAB\right)\cap\left(SAD\right)=SA\)
b: Gọi O là giao điểm của AC và BD trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
c: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC