
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{AOD}\) chung
OD=OB
Do đó:ΔOAD=ΔOCB
Suy ra: AD=BC
b: Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó:ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó:ΔOEB=ΔOED
SUy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc BOD
d: Xét ΔOBD có OA/OB=OC/OD
nên AC//BD

a: a\(\perp\)IK
b\(\perp\)IK
Do đó: a//b
b: Ta có: a//b
=>\(\widehat{GHE}+\widehat{HEK}=180^0\)(hai góc trong cùng phía)
Ta có: \(\widehat{HEK}=\widehat{DEF}\)(hai góc đối đỉnh)
mà \(\widehat{DEF}=62^0\)
nên \(\widehat{HEK}=62^0\)
=>\(\widehat{GHE}=180^0-62^0=118^0\)
c: ta có: ΔKIE vuông tại K
=>\(\widehat{KIE}+\widehat{KEI}=90^0\)
=>\(\widehat{KIE}+62^0=90^0\)
=>\(\widehat{KIE}=28^0\)

Bài 2:
=10-7=3
Bài 3:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{7}=\dfrac{y}{3}=\dfrac{x-y}{7-3}=\dfrac{-16}{4}=-4\)
Do đó: x=-28; y=-12
Ax // BC // Dy. A= 55°
a) Tính B = ?
b) Tìm số đo của C để AB//CD. Khi đó tính D =?
Giúp tớ với huhu :(


a) Có DE < DF( 5cm < 12cm)
->góc F< góc E
b) áp dụng đl pytago:
EF^2=DE^2+DF^2=5^2+12^2=169
= > EF=13 (cm)
tam giác DEF có DM là trung tuyến(M là trung điểm của EF) ứng với cạnh huyền
=> DM=EM=MF=EF/2=13/2=6,5cm

Lấy điểm D sao cho điểm F là trung điểm của DE\(\Rightarrow\)\(EF=DF=\dfrac{1}{2}DE\), nối E với C
\(\text{Xét }\Delta AEF\text{ và }\Delta CDF\text{ có:}\)
\(AF=FC\left(gt\right)\left(1\right)\)
\(\widehat{F_1}=\widehat{F_2}\left(\text{đối đỉnh}\right)\left(2\right)\)
\(EF=DF\left(\text{hình vẽ}\right)\left(3\right)\)
\(\text{Từ (1),(2) và (3)}\Rightarrow\Delta AEF=\Delta CDF\left(c.g.c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}AE=CD\left(\text{2 cạnh tương ứng}\right),\text{mà }AE=BE\left(gt\right)\Rightarrow BE=CD\\\widehat{EAF}=\widehat{DCF}\left(\text{2 góc tương ứng}\right)\left(5\right)\end{matrix}\right.\)
\(\text{Mà 2 góc này ở vị trí so le trong của đường thẳng AE và CD}\left(6\right)\)
\(\text{Từ (5) và (6)}\Rightarrow AE\text{//}CD\left(\text{dấu hiệu nhận biết}\right)\)
\(\text{Hay }BE\text{//}CD\left(\text{do A,E,B thẳng hàng}\right)\)
\(\Rightarrow\widehat{BEC}=\widehat{DCE}\left(\text{so le trong}\right)\)
\(\text{Xét }\Delta BEC\text{ và }\Delta DCE\text{ có:}\)
\(BE=DC\left(cmt\right)\left(7\right)\)
\(\widehat{BEC}=\widehat{DCE}\left(cmt\right)\left(8\right)\)
\(\text{CE chung}\left(9\right)\)
\(\text{Từ (7),(8) và (9)}\Rightarrow\Delta BEC=\Delta DCE\left(c.g.c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}BC=DE\left(\text{2 cạnh tương ứng}\right),\text{Mà }EF=\dfrac{1}{2}DE\Rightarrow EF=\dfrac{1}{2}BC\Rightarrow EF=\dfrac{BC}{2}\left(đpcm\right)\\\widehat{BCE}=\widehat{DEC}\left(\text{2 góc tương ứng}\right)\text{Hay }\widehat{BCE}=\widehat{FEC}\left(10\right)\end{matrix}\right.\)
\(\text{Mà 2 góc này ở vị trí so le trong của 2 đường thẳng BC và EF}\left(11\right)\)
\(\text{Từ (10) và (11)}\Rightarrow BC\text{//}EF\left(\text{dấu hiệu nhận biết}\right)\left(đpcm\right)\)
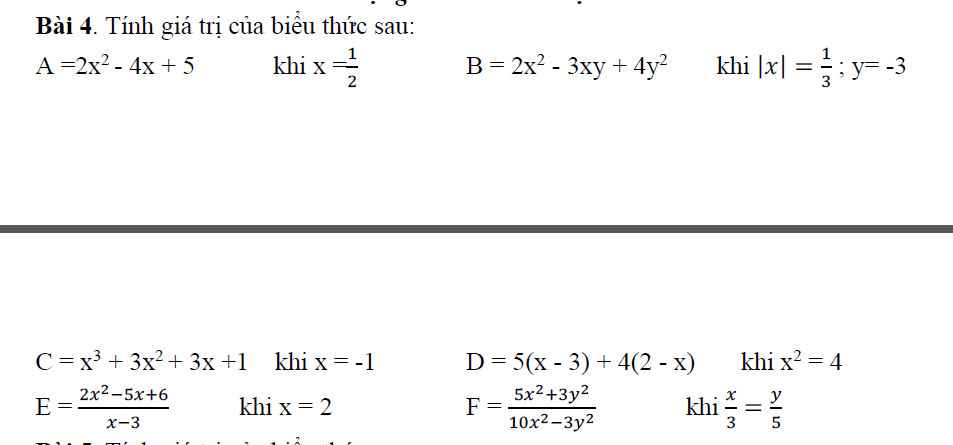 giúp tớ câu B, D, E, F với huhu
giúp tớ câu B, D, E, F với huhu
b,\(\left|x\right|=\dfrac{1}{3}\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Thay \(x=\dfrac{1}{3},y=-3\) vào B ta có:
\(B=2x^2-3xy+4y^2=2.\left(\dfrac{1}{3}\right)^2-3.\dfrac{1}{3}.\left(-3\right)+4.\left(-3\right)^2=2.\dfrac{1}{9}+3+4.9=\dfrac{2}{9}+3+36=\dfrac{353}{9}\)
Thay \(x=\dfrac{-1}{3},y=-3\) vào B ta có:
\(B=2x^2-3xy+4y^2=2.\left(\dfrac{-1}{3}\right)^2-3.\dfrac{-1}{3}.\left(-3\right)+4.\left(-3\right)^2=2.\dfrac{1}{9}-3+4.9=\dfrac{2}{9}-3+36=\dfrac{299}{9}\)
d,\(D=5\left(x-3\right)+4\left(2-x\right)=5x-15+8-4x=x-7\)
\(x^2=4\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
Thay x=-2 vào D ta có:
\(D=x-7=-2-7=-9\)
Thay x=2 vào D ta có:
\(D=x-7=2-7=-5\)
e,Thay x=2 vào E ta có:
\(\dfrac{2x^2-5x+6}{x-3}=\dfrac{2.2^2-5.2+6}{2-3}=\dfrac{8-10+6}{-1}=-4\)
f, Đặt \(\dfrac{x}{3}=\dfrac{y}{5}=k\Rightarrow x=3k,y=5k\)
\(F=\dfrac{5x^2+3y^2}{10x^2-3y^2}=\dfrac{5.\left(3k\right)^2+3.\left(5k\right)^2}{10.\left(3k\right)^2-3.\left(5k\right)^2}=\dfrac{5.9k^2+3.25k^2}{10.9k^2-3.25k^2}=\dfrac{45k^2+75k^2}{90k^2-75k^2}=\dfrac{120}{15}=8\)