
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vd là Hình chữ nhật là có cả đối xứng trục và đối xứng tâm
Hình vuông cũng vậy
Hình thang cân thì có đối xứng trục nhưng không có đối xứng tâm

1. x2-x-2
=(x2-2x)+(x-2)
= x(x-2)+(x-2)
= (x+1)(x-2)
2.x2-3x+2
=x2-x-2x+2
=(x2-x)-(2x-2)
=x(x-1)-2(x-1)
=(x-2)(x-1)
3.-x2-2x+3
=3-2x-x2
=3+x-3x-x2
=(3+x)-(3x+x2)
=(3+x)-x(3+x)
=(1-x)(3+x)
4. x2-5x+4
=x2-x-4x+4
=(x2-x)-(4x-4)
=x(x-1)-4(x-1)
=(x-1)(x-4)
5. x2-5x+6
=x2-2x-3x+6
=(x2-2x)-(3x-6)
=x(x-2)-3(x-2)
=(x-2)(x-3)
6.x2-6x+5
=(x2-x)-(5x-5)
=x(x-1)-5(x-1)
=(x-1)(x-5)
7.x2-7x+12
=(x2-3x)-(4x-12)
=x(x-3)-4(x-3)
=(x-4)(x-3)
8.-x2+7x-12
=(-x2+3x)+(4x-12)
=-x(x-3)+4(x-3)
=(4-x)(x-3)
9.x2-3x-4
=(x2+x)-(4x+4)
=x(x+1)-4(x+1)
=(x-4)(x+1)
mik làm 1 nửa thôi dài quá

a: Xét ΔACE có
D là trung điểm của AC
O là trung điểm của EC
Do đó: DO là đường trung bình
=>DO//AE
hay DO//AB(1)
Xét ΔECB có
O là trung điểm của EC
M là trung điểm của BC
Do đó: OM là đường trung bình
=>OM//EB và OM=EB/2(3)
hay OM//AB(2)
Từ (1) và (2) suy ra M,O,D thẳng hàng
b: Xét ΔEDC có
N là trung điểm của DE
O là trung điểm của EC
Do đó: NO là đường trung bình
=>NO=DC/2=EB/2(4)
Từ (3) và (4) suy ra OM=ON
hay ΔOMN cân tại O

11)\(\dfrac{3x+1}{x-5}+\dfrac{2x}{x-5}=\dfrac{3x+2x+1}{x-5}=\dfrac{5x+1}{x-5}\)
12)\(\dfrac{4-x^2}{x-3}+\dfrac{2}{x^2-9}=\dfrac{4-x^2}{x-3}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{\left(4-x^2\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{2+\left(2-x\right)\left(2+x\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
13)
\(\dfrac{3}{4x-2}+\dfrac{2x}{4x^2-1}=\dfrac{3}{2\left(2x-1\right)}+\dfrac{2x}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{3\left(2x+1\right)}{2\left(2x-1\right)\left(2x+1\right)}+\dfrac{2.2x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{6x+3+4x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{10x+3}{2\left(2x-1\right)\left(2x+1\right)}\)
14)
\(\dfrac{2x+1}{2x-4}+\dfrac{5}{x^2-4}=\dfrac{2x+1}{2\left(x-2\right)}+\dfrac{5}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(2x+1\right)\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\dfrac{5.2}{2\left(x-2\right)\left(x+2\right)}=\dfrac{2x^2+5x+12}{2\left(x-2\right)\left(x+2\right)}\)

1) Đặc điểm oxit: 2 nguyên tố (MxOy)
2) Oxit gồm 2 loại:
+ Oxit axit: chứa phi kim (hoặc một số kim loại có hóa trị cao ví dụ: Mn (VII), Cr (VII)…) và tương ứng với 1 axit.
VD: SO3 có axit tương ứng là H2SO4.
+ Oxit bazơ: chứa kim loại và tương ứng với 1 bazơ.
VD: K2O có bazơ tương ứng là KOH.
3) Tên gọi:
Cách gọi chung: Tên nguyên tố + oxit
+ Với kim loại nhiều hóa trị:
Tên oxit bazơ: Tên kim loại (kèm hóa trị) + oxit
+ Với phi kim nhiều hóa trị:
Tên oxit axit: Tên phi kim + oxit
(kèm tiền tố chỉ số nguyên tử phi kim) (kèm tiền tố chỉ số nguyên tử oxi)
Các tiền tố: 2 – đi; 3 – tri; 4 – têtra; 5 – penta.
Ví dụ
Phân loại các oxit sau và gọi tên các oxit đó.
SO2, K2O, MgO, P2O5, N2O5, Al2O3, Fe2O3, CO2.
Axit
1. Khái niệm
- VD: HCl, H2S, H2SO4 , HNO3, H2CO3, H3PO4.
- TPPT: Có 1 hay nhiều nguyên tử hiđro liên kết với gốc axit (- Cl, =S, =SO4, -NO3...)
- Phân tử axit gồm có một hay nhiều nguyên tử hiđro liên kết với gốc axit, các nguyên tử hiđro này có thể thay thế bằng các nguyên tử kim loại.
2. Công thức hoá học
- Gồm một hay nhiều nguyên tử hiđro và gốc axit.
Công thức chung: HnA.
Trong đó: - H: là nguyên tử hiđro.
- A: là gốc axit.
3. Phân loại
- 2 loại:
+ Axit không có oxi: HCl, H2S, HBr, HI, HF...
+ Axit có oxi: H2SO4, HNO3, H3PO4, H2CO3...
4. Tên gọi
a. Axit không có oxi
Tên axit : Axit + tên phi kim + hiđric.
VD : - HCl : Axit clohiđric.
- H2S : Axit sunfuhiđric.


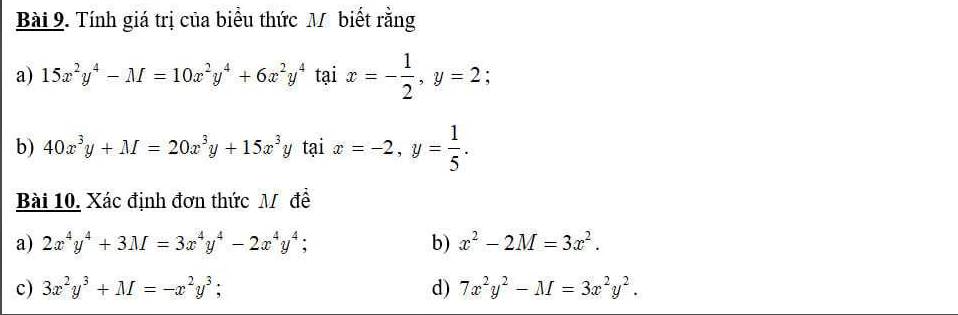


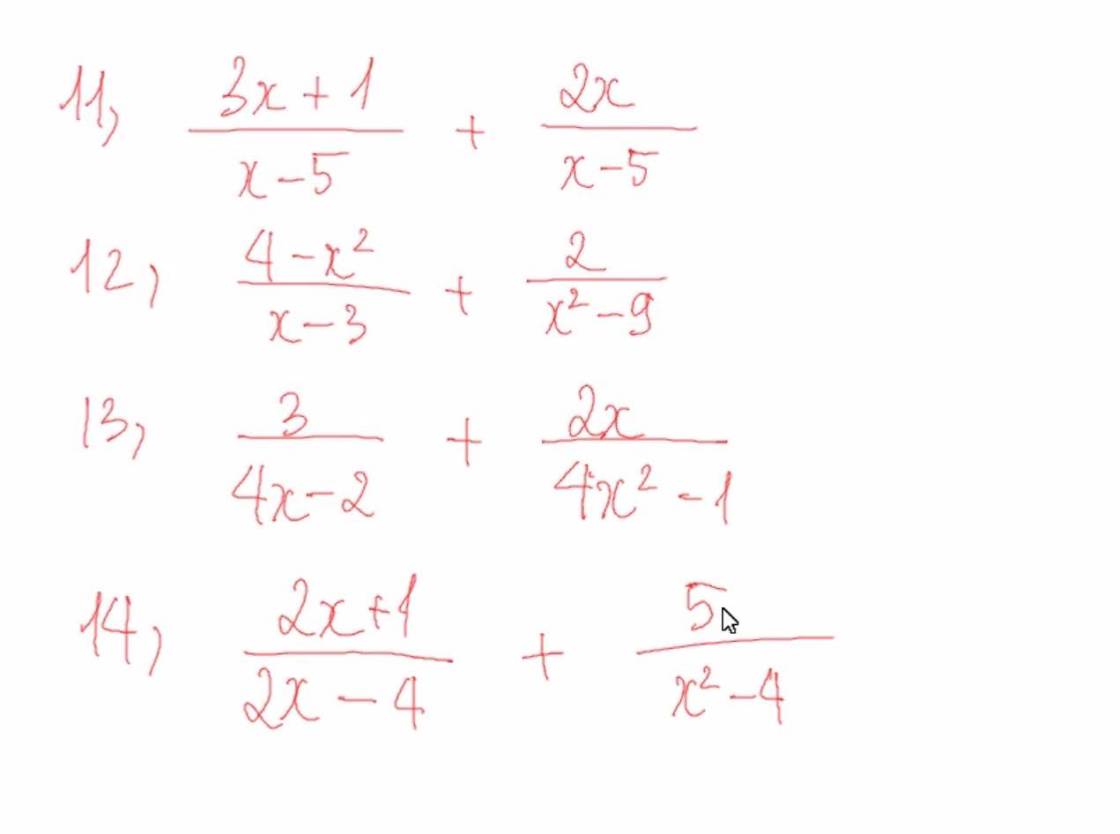
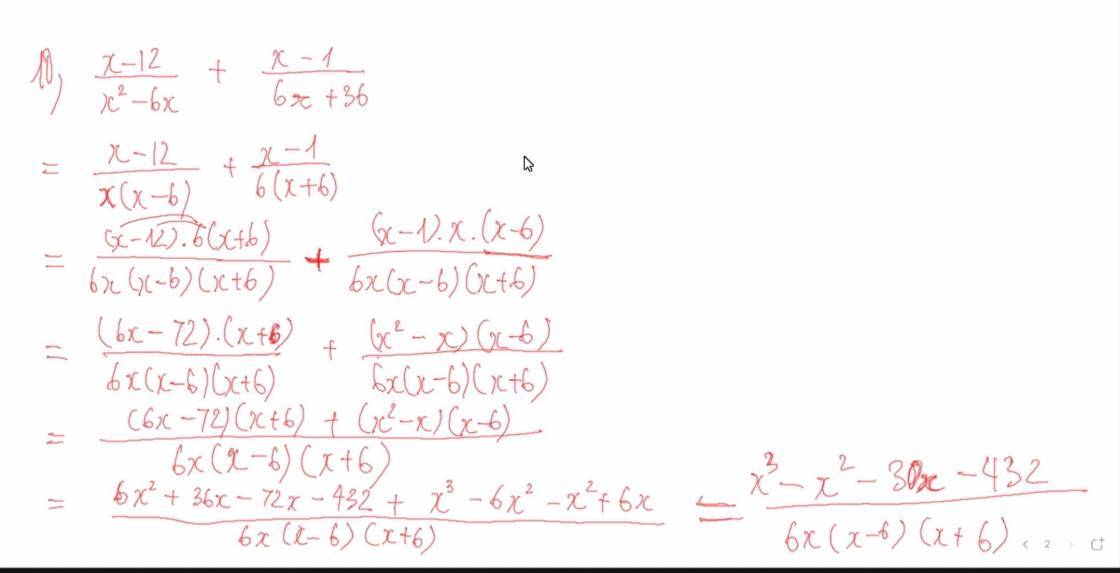
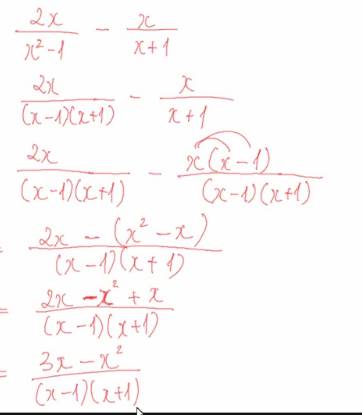
Bài 9:
\(a,15x^2y^4-M=10x^2y^4+6x^2y^4\\ \Rightarrow M=15x^2y^4-10x^2y^4-6x^2y^4=-x^2y^4\\ Thế.x=-\dfrac{1}{2}.và.y=2.vào.M.thu.gọn:M=-x^2y^4=-\left(-\dfrac{1}{2}\right)^2.2^4=-\dfrac{1}{4}.16=-4\\ b,40x^3y+M=20x^3y+15x^3y\\ \Rightarrow M=20x^3y+15x^3y-40x^3y=-5x^3y\\ Thế.x=-2.và.y=\dfrac{1}{5}.vào.M.thu.gọn:M=-5x^3y=-5.\left(-2\right)^3.\dfrac{1}{5}=-5.8.\dfrac{1}{5}=-8\)